
|
Welcome to ShortScience.org! |


|
- ShortScience.org is a platform for post-publication discussion aiming to improve accessibility and reproducibility of research ideas.
- The website has 1584 public summaries, mostly in machine learning, written by the community and organized by paper, conference, and year.
- Reading summaries of papers is useful to obtain the perspective and insight of another reader, why they liked or disliked it, and their attempt to demystify complicated sections.
- Also, writing summaries is a good exercise to understand the content of a paper because you are forced to challenge your assumptions when explaining it.
- Finally, you can keep up to date with the flood of research by reading the latest summaries on our Twitter and Facebook pages.
Teaching Machines to Read and Comprehend
Hermann, Karl Moritz and Kociský, Tomás and Grefenstette, Edward and Espeholt, Lasse and Kay, Will and Suleyman, Mustafa and Blunsom, Phil
Neural Information Processing Systems Conference - 2015 via Local Bibsonomy
Keywords: dblp
Hermann, Karl Moritz and Kociský, Tomás and Grefenstette, Edward and Espeholt, Lasse and Kay, Will and Suleyman, Mustafa and Blunsom, Phil
Neural Information Processing Systems Conference - 2015 via Local Bibsonomy
Keywords: dblp
|
[link]
This paper deals with the formal question of machine reading. It proposes a novel methodology for automatic dataset building for machine reading model evaluation. To do so, the authors leverage on news resources that are equipped with a summary to generate a large number of questions about articles by replacing the named entities of it. Furthermore a attention enhanced LSTM inspired reading model is proposed and evaluated. The paper is well-written and clear, the originality seems to lie on two aspects. First, an original methodology of question answering dataset creation, where context-query-answer triples are automatically extracted from news feeds. Such proposition can be considered as important because it opens the way for large model learning and evaluation. The second contribution is the addition of an attention mechanism to an LSTM reading model. the empirical results seem to show relevant improvement with respect to an up-to-date list of machine reading models. Given the lack of an appropriate dataset, the author provides a new dataset which scraped CNN and Daily Mail, using both the full text and abstract summaries/bullet points. The dataset was then anonymised (i.e. entity names removed). Next the author presents a two novel Deep long-short term memory models which perform well on the Cloze query task.  |
Self-Normalizing Neural Networks
Günter Klambauer and Thomas Unterthiner and Andreas Mayr and Sepp Hochreiter
arXiv e-Print archive - 2017 via Local arXiv
Keywords: cs.LG, stat.ML
First published: 2017/06/08 (6 years ago)
Abstract: Deep Learning has revolutionized vision via convolutional neural networks (CNNs) and natural language processing via recurrent neural networks (RNNs). However, success stories of Deep Learning with standard feed-forward neural networks (FNNs) are rare. FNNs that perform well are typically shallow and, therefore cannot exploit many levels of abstract representations. We introduce self-normalizing neural networks (SNNs) to enable high-level abstract representations. While batch normalization requires explicit normalization, neuron activations of SNNs automatically converge towards zero mean and unit variance. The activation function of SNNs are "scaled exponential linear units" (SELUs), which induce self-normalizing properties. Using the Banach fixed-point theorem, we prove that activations close to zero mean and unit variance that are propagated through many network layers will converge towards zero mean and unit variance -- even under the presence of noise and perturbations. This convergence property of SNNs allows to (1) train deep networks with many layers, (2) employ strong regularization, and (3) to make learning highly robust. Furthermore, for activations not close to unit variance, we prove an upper and lower bound on the variance, thus, vanishing and exploding gradients are impossible. We compared SNNs on (a) 121 tasks from the UCI machine learning repository, on (b) drug discovery benchmarks, and on (c) astronomy tasks with standard FNNs and other machine learning methods such as random forests and support vector machines. SNNs significantly outperformed all competing FNN methods at 121 UCI tasks, outperformed all competing methods at the Tox21 dataset, and set a new record at an astronomy data set. The winning SNN architectures are often very deep. Implementations are available at: github.com/bioinf-jku/SNNs.
more
less
Günter Klambauer and Thomas Unterthiner and Andreas Mayr and Sepp Hochreiter
arXiv e-Print archive - 2017 via Local arXiv
Keywords: cs.LG, stat.ML
First published: 2017/06/08 (6 years ago)
Abstract: Deep Learning has revolutionized vision via convolutional neural networks (CNNs) and natural language processing via recurrent neural networks (RNNs). However, success stories of Deep Learning with standard feed-forward neural networks (FNNs) are rare. FNNs that perform well are typically shallow and, therefore cannot exploit many levels of abstract representations. We introduce self-normalizing neural networks (SNNs) to enable high-level abstract representations. While batch normalization requires explicit normalization, neuron activations of SNNs automatically converge towards zero mean and unit variance. The activation function of SNNs are "scaled exponential linear units" (SELUs), which induce self-normalizing properties. Using the Banach fixed-point theorem, we prove that activations close to zero mean and unit variance that are propagated through many network layers will converge towards zero mean and unit variance -- even under the presence of noise and perturbations. This convergence property of SNNs allows to (1) train deep networks with many layers, (2) employ strong regularization, and (3) to make learning highly robust. Furthermore, for activations not close to unit variance, we prove an upper and lower bound on the variance, thus, vanishing and exploding gradients are impossible. We compared SNNs on (a) 121 tasks from the UCI machine learning repository, on (b) drug discovery benchmarks, and on (c) astronomy tasks with standard FNNs and other machine learning methods such as random forests and support vector machines. SNNs significantly outperformed all competing FNN methods at 121 UCI tasks, outperformed all competing methods at the Tox21 dataset, and set a new record at an astronomy data set. The winning SNN architectures are often very deep. Implementations are available at: github.com/bioinf-jku/SNNs.
|
[link]
_Objective:_ Design Feed-Forward Neural Network (fully connected) that can be trained even with very deep architectures.
* _Dataset:_ [MNIST](yann.lecun.com/exdb/mnist/), [CIFAR10](https://www.cs.toronto.edu/%7Ekriz/cifar.html), [Tox21](https://tripod.nih.gov/tox21/challenge/) and [UCI tasks](https://archive.ics.uci.edu/ml/datasets/optical+recognition+of+handwritten+digits).
* _Code:_ [here](https://github.com/bioinf-jku/SNNs)
## Inner-workings:
They introduce a new activation functio the Scaled Exponential Linear Unit (SELU) which has the nice property of making neuron activations converge to a fixed point with zero-mean and unit-variance.
They also demonstrate that upper and lower bounds and the variance and mean for very mild conditions which basically means that there will be no exploding or vanishing gradients.
The activation function is:
[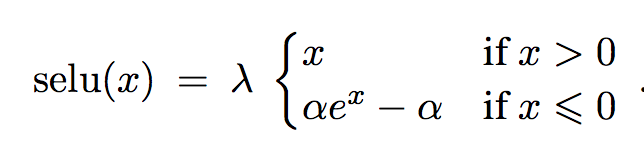](https://user-images.githubusercontent.com/17261080/27125901-1a4f7276-50f6-11e7-857d-ebad1ac94789.png)
With specific parameters for alpha and lambda to ensure the previous properties. The tensorflow impementation is:
def selu(x):
alpha = 1.6732632423543772848170429916717
scale = 1.0507009873554804934193349852946
return scale*np.where(x>=0.0, x, alpha*np.exp(x)-alpha)
They also introduce a new dropout (alpha-dropout) to compensate for the fact that [](https://user-images.githubusercontent.com/17261080/27126174-e67d212c-50f6-11e7-8952-acad98b850be.png)
## Results:
Batch norm becomes obsolete and they are also able to train deeper architectures. This becomes a good choice to replace shallow architectures where random forest or SVM used to be the best results. They outperform most other techniques on small datasets.
[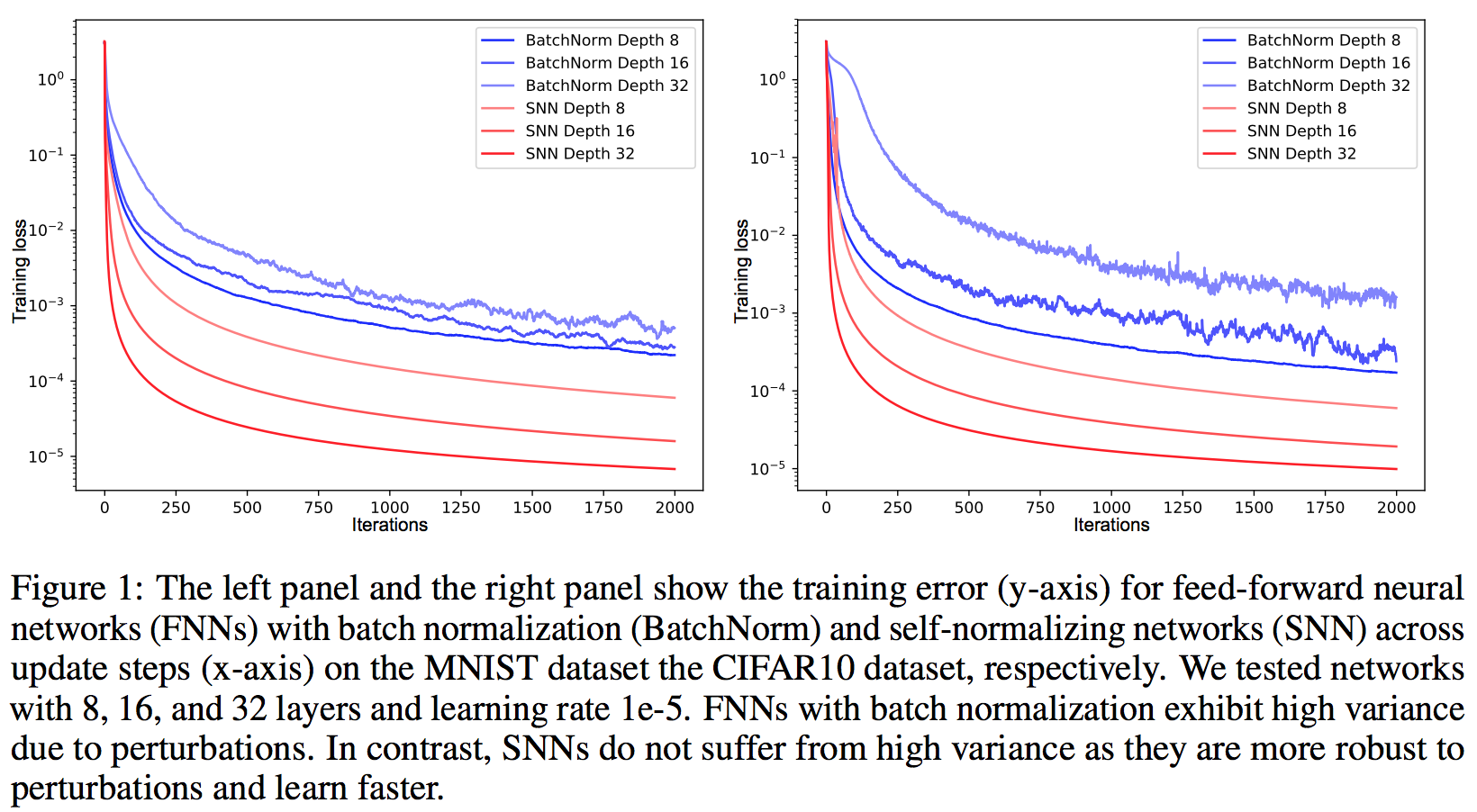](https://user-images.githubusercontent.com/17261080/27125798-bd04c256-50f5-11e7-8a74-b3b6a3fe82ee.png)
Might become a new standard for fully-connected activations in the future.
 |
Recurrent Batch Normalization
Cooijmans, Tim and Ballas, Nicolas and Laurent, César and Courville, Aaron
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Cooijmans, Tim and Ballas, Nicolas and Laurent, César and Courville, Aaron
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
This paper describes how to apply the idea of batch normalization (BN) successfully to recurrent neural networks, specifically to LSTM networks. The technique involves the 3 following ideas: **1) Careful initialization of the BN scaling parameter.** While standard practice is to initialize it to 1 (to have unit variance), they show that this situation creates problems with the gradient flow through time, which vanishes quickly. A value around 0.1 (used in the experiments) preserves gradient flow much better. **2) Separate BN for the "hiddens to hiddens pre-activation and for the "inputs to hiddens" pre-activation.** In other words, 2 separate BN operators are applied on each contributions to the pre-activation, before summing and passing through the tanh and sigmoid non-linearities. **3) Use of largest time-step BN statistics for longer test-time sequences.** Indeed, one issue with applying BN to RNNs is that if the input sequences have varying length, and if one uses per-time-step mean/variance statistics in the BN transformation (which is the natural thing to do), it hasn't been clear how do deal with the last time steps of longer sequences seen at test time, for which BN has no statistics from the training set. The paper shows evidence that the pre-activation statistics tend to gradually converge to stationary values over time steps, which supports the idea of simply using the training set's last time step statistics. Among these ideas, I believe the most impactful idea is 1). The papers mentions towards the end that improper initialization of the BN scaling parameter probably explains previous failed attempts to apply BN to recurrent networks. Experiments on 4 datasets confirms the method's success. **My two cents** This is an excellent development for LSTMs. BN has had an important impact on our success in training deep neural networks, and this approach might very well have a similar impact on the success of LSTMs in practice.  |
Mask R-CNN
He, Kaiming and Gkioxari, Georgia and Dollár, Piotr and Girshick, Ross B.
arXiv e-Print archive - 2017 via Local Bibsonomy
Keywords: dblp
He, Kaiming and Gkioxari, Georgia and Dollár, Piotr and Girshick, Ross B.
arXiv e-Print archive - 2017 via Local Bibsonomy
Keywords: dblp
|
[link]
Mask RCNN takes off from where Faster RCNN left, with some augmentations aimed at bettering instance segmentation (which was out of scope for FRCNN). Instance segmentation was achieved remarkably well in *DeepMask* , *SharpMask* and later *Feature Pyramid Networks* (FPN). Faster RCNN was not designed for pixel-to-pixel alignment between network inputs and outputs. This is most evident in how RoIPool , the de facto core operation for attending to instances, performs coarse spatial quantization for feature extraction. Mask RCNN fixes that by introducing RoIAlign in place of RoIPool. #### Methodology Mask RCNN retains most of the architecture of Faster RCNN. It adds the a third branch for segmentation. The third branch takes the output from RoIAlign layer and predicts binary class masks for each class. ##### Major Changes and intutions **Mask prediction** Mask prediction segmentation predicts a binary mask for each RoI using fully convolution - and the stark difference being usage of *sigmoid* activation for predicting final mask instead of *softmax*, implies masks don't compete with each other. This *decouples* segmentation from classification. The class prediction branch is used for class prediction and for calculating loss, the mask of predicted loss is used calculating Lmask. Also, they show that a single class agnostic mask prediction works almost as effective as separate mask for each class, thereby supporting their method of decoupling classification from segmentation **RoIAlign** RoIPool first quantizes a floating-number RoI to the discrete granularity of the feature map, this quantized RoI is then subdivided into spatial bins which are themselves quantized, and finally feature values covered by each bin are aggregated (usually by max pooling). Instead of quantization of the RoI boundaries or bin bilinear interpolation is used to compute the exact values of the input features at four regularly sampled locations in each RoI bin, and aggregate the result (using max or average). **Backbone architecture** Faster RCNN uses a VGG like structure for extracting features from image, weights of which were shared among RPN and region detection layers. Herein, authors experiment with 2 backbone architectures - ResNet based VGG like in FRCNN and ResNet based [FPN](http://www.shortscience.org/paper?bibtexKey=journals/corr/LinDGHHB16) based. FPN uses convolution feature maps from previous layers and recombining them to produce pyramid of feature maps to be used for prediction instead of single-scale feature layer (final output of conv layer before connecting to fc layers was used in Faster RCNN) **Training Objective** The training objective looks like this  Lmask is the addition from Faster RCNN. The method to calculate was mentioned above #### Observation Mask RCNN performs significantly better than COCO instance segmentation winners *without any bells and whiskers*. Detailed results are available in the paper  |
Generating Images with Perceptual Similarity Metrics based on Deep Networks
Alexey Dosovitskiy and Thomas Brox
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.LG, cs.CV, cs.NE
First published: 2016/02/08 (8 years ago)
Abstract: Image-generating machine learning models are typically trained with loss functions based on distance in the image space. This often leads to over-smoothed results. We propose a class of loss functions, which we call deep perceptual similarity metrics (DeePSiM), that mitigate this problem. Instead of computing distances in the image space, we compute distances between image features extracted by deep neural networks. This metric better reflects perceptually similarity of images and thus leads to better results. We show three applications: autoencoder training, a modification of a variational autoencoder, and inversion of deep convolutional networks. In all cases, the generated images look sharp and resemble natural images.
more
less
Alexey Dosovitskiy and Thomas Brox
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.LG, cs.CV, cs.NE
First published: 2016/02/08 (8 years ago)
Abstract: Image-generating machine learning models are typically trained with loss functions based on distance in the image space. This often leads to over-smoothed results. We propose a class of loss functions, which we call deep perceptual similarity metrics (DeePSiM), that mitigate this problem. Instead of computing distances in the image space, we compute distances between image features extracted by deep neural networks. This metric better reflects perceptually similarity of images and thus leads to better results. We show three applications: autoencoder training, a modification of a variational autoencoder, and inversion of deep convolutional networks. In all cases, the generated images look sharp and resemble natural images.
|
[link]
* The authors define in this paper a special loss function (DeePSiM), mostly for autoencoders.
* Usually one would use a MSE of euclidean distance as the loss function for an autoencoder. But that loss function basically always leads to blurry reconstructed images.
* They add two new ingredients to the loss function, which results in significantly sharper looking images.
### How
* Their loss function has three components:
* Euclidean distance in image space (i.e. pixel distance between reconstructed image and original image, as usually used in autoencoders)
* Euclidean distance in feature space. Another pretrained neural net (e.g. VGG, AlexNet, ...) is used to extract features from the original and the reconstructed image. Then the euclidean distance between both vectors is measured.
* Adversarial loss, as usually used in GANs (generative adversarial networks). The autoencoder is here treated as the GAN-Generator. Then a second network, the GAN-Discriminator is introduced. They are trained in the typical GAN-fashion. The loss component for DeePSiM is the loss of the Discriminator. I.e. when reconstructing an image, the autoencoder would learn to reconstruct it in a way that lets the Discriminator believe that the image is real.
* Using the loss in feature space alone would not be enough as that tends to lead to overpronounced high frequency components in the image (i.e. too strong edges, corners, other artefacts).
* To decrease these high frequency components, a "natural image prior" is usually used. Other papers define some function by hand. This paper uses the adversarial loss for that (i.e. learns a good prior).
* Instead of training a full autoencoder (encoder + decoder) it is also possible to only train a decoder and feed features - e.g. extracted via AlexNet - into the decoder.
### Results
* Using the DeePSiM loss with a normal autoencoder results in sharp reconstructed images.
* Using the DeePSiM loss with a VAE to generate ILSVRC-2012 images results in sharp images, which are locally sound, but globally don't make sense. Simple euclidean distance loss results in blurry images.
* Using the DeePSiM loss when feeding only image space features (extracted via AlexNet) into the decoder leads to high quality reconstructions. Features from early layers will lead to more exact reconstructions.
* One can again feed extracted features into the network, but then take the reconstructed image, extract features of that image and feed them back into the network. When using DeePSiM, even after several iterations of that process the images still remain semantically similar, while their exact appearance changes (e.g. a dog's fur color might change, counts of visible objects change).

*Images generated with a VAE using DeePSiM loss.*

*Images reconstructed from features fed into the network. Different AlexNet layers (conv5 - fc8) were used to generate the features. Earlier layers allow more exact reconstruction.*

*First, images are reconstructed from features (AlexNet, layers conv5 - fc8 as columns). Then, features of the reconstructed images are fed back into the network. That is repeated up to 8 times (rows). Images stay semantically similar, but their appearance changes.*
--------------------
### Rough chapter-wise notes
* (1) Introduction
* Using a MSE of euclidean distances for image generation (e.g. autoencoders) often results in blurry images.
* They suggest a better loss function that cares about the existence of features, but not as much about their exact translation, rotation or other local statistics.
* Their loss function is based on distances in suitable feature spaces.
* They use ConvNets to generate those feature spaces, as these networks are sensitive towards important changes (e.g. edges) and insensitive towards unimportant changes (e.g. translation).
* However, naively using the ConvNet features does not yield good results, because the networks tend to project very different images onto the same feature vectors (i.e. they are contractive). That leads to artefacts in the generated images.
* Instead, they combine the feature based loss with GANs (adversarial loss). The adversarial loss decreases the negative effects of the feature loss ("natural image prior").
* (3) Model
* A typical choice for the loss function in image generation tasks (e.g. when using an autoencoders) would be squared euclidean/L2 loss or L1 loss.
* They suggest a new class of losses called "DeePSiM".
* We have a Generator `G`, a Discriminator `D`, a feature space creator `C` (takes an image, outputs a feature space for that image), one (or more) input images `x` and one (or more) target images `y`. Input and target image can be identical.
* The total DeePSiM loss is a weighted sum of three components:
* Feature loss: Squared euclidean distance between the feature spaces of (1) input after fed through G and (2) the target image, i.e. `||C(G(x))-C(y)||^2_2`.
* Adversarial loss: A discriminator is introduced to estimate the "fakeness" of images generated by the generator. The losses for D and G are the standard GAN losses.
* Pixel space loss: Classic squared euclidean distance (as commonly used in autoencoders). They found that this loss stabilized their adversarial training.
* The feature loss alone would create high frequency artefacts in the generated image, which is why a second loss ("natural image prior") is needed. The adversarial loss fulfills that role.
* Architectures
* Generator (G):
* They define different ones based on the task.
* They all use up-convolutions, which they implement by stacking two layers: (1) a linear upsampling layer, then (2) a normal convolutional layer.
* They use leaky ReLUs (alpha=0.3).
* Comparators (C):
* They use variations of AlexNet and Exemplar-CNN.
* They extract the features from different layers, depending on the experiment.
* Discriminator (D):
* 5 convolutions (with some striding; 7x7 then 5x5, afterwards 3x3), into average pooling, then dropout, then 2x linear, then 2-way softmax.
* Training details
* They use Adam with learning rate 0.0002 and normal momentums (0.9 and 0.999).
* They temporarily stop the discriminator training when it gets too good.
* Batch size was 64.
* 500k to 1000k batches per training.
* (4) Experiments
* Autoencoder
* Simple autoencoder with an 8x8x8 code layer between encoder and decoder (so actually more values than in the input image?!).
* Encoder has a few convolutions, decoder a few up-convolutions (linear upsampling + convolution).
* They train on STL-10 (96x96) and take random 64x64 crops.
* Using for C AlexNet tends to break small structural details, using Exempler-CNN breaks color details.
* The autoencoder with their loss tends to produce less blurry images than the common L2 and L1 based losses.
* Training an SVM on the 8x8x8 hidden layer performs significantly with their loss than L2/L1. That indicates potential for unsupervised learning.
* Variational Autoencoder
* They replace part of the standard VAE loss with their DeePSiM loss (keeping the KL divergence term).
* Everything else is just like in a standard VAE.
* Samples generated by a VAE with normal loss function look very blurry. Samples generated with their loss function look crisp and have locally sound statistics, but still (globally) don't really make any sense.
* Inverting AlexNet
* Assume the following variables:
* I: An image
* ConvNet: A convolutional network
* F: The features extracted by a ConvNet, i.e. ConvNet(I) (feaures in all layers, not just the last one)
* Then you can invert the representation of a network in two ways:
* (1) An inversion that takes an F and returns roughly the I that resulted in F (it's *not* key here that ConvNet(reconstructed I) returns the same F again).
* (2) An inversion that takes an F and projects it to *some* I so that ConvNet(I) returns roughly the same F again.
* Similar to the autoencoder cases, they define a decoder, but not encoder.
* They feed into the decoder a feature representation of an image. The features are extracted using AlexNet (they try the features from different layers).
* The decoder has to reconstruct the original image (i.e. inversion scenario 1). They use their DeePSiM loss during the training.
* The images can be reonstructed quite well from the last convolutional layer in AlexNet. Chosing the later fully connected layers results in more errors (specifially in the case of the very last layer).
* They also try their luck with the inversion scenario (2), but didn't succeed (as their loss function does not care about diversity).
* They iteratively encode and decode the same image multiple times (probably means: image -> features via AlexNet -> decode -> reconstructed image -> features via AlexNet -> decode -> ...). They observe, that the image does not get "destroyed", but rather changes semantically, e.g. three apples might turn to one after several steps.
* They interpolate between images. The interpolations are smooth.
 |












