* ELUs are an activation function
  * The are most similar to LeakyReLUs and PReLUs

### How (formula)
  * f(x):
    * `if x >= 0: x`
    * `else: alpha(exp(x)-1)`
  * f'(x) / Derivative:
    * `if x >= 0: 1`
    * `else: f(x) + alpha`
  * `alpha` defines at which negative value the ELU saturates.
  * E. g. `alpha=1.0` means that the minimum value that the ELU can reach is `-1.0`
  * LeakyReLUs however can go to `-Infinity`, ReLUs can't go below 0.

![ELUs vs LeakyReLUs vs ReLUs](https://raw.githubusercontent.com/aleju/papers/master/neural-nets/images/ELUs__slopes.png?raw=true "ELUs vs LeakyReLUs vs ReLUs")

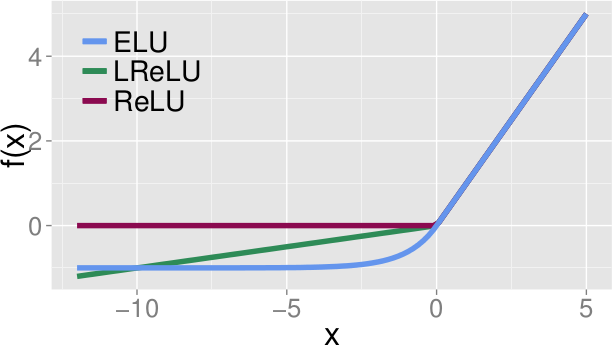
*Form of ELUs(alpha=1.0) vs LeakyReLUs vs ReLUs.*


### Why
  * They derive from the unit natural gradient that a network learns faster, if the mean activation of each neuron is close to zero.
  * ReLUs can go above 0, but never below. So their mean activation will usually be quite a bit above 0, which should slow down learning.
  * ELUs, LeakyReLUs and PReLUs all have negative slopes, so their mean activations should be closer to 0.
  * In contrast to LeakyReLUs and PReLUs, ELUs saturate at a negative value (usually -1.0).
  * The authors think that is good, because it lets ELUs encode the degree of presence of input concepts, while they do not quantify the degree of absence.
  * So ELUs can measure the presence of concepts quantitatively, but the absence only qualitatively.
  * They think that this makes ELUs more robust to noise.

### Results
  * In their tests on MNIST, CIFAR-10, CIFAR-100 and ImageNet, ELUs perform (nearly always) better than ReLUs and LeakyReLUs.
  * However, they don't test PReLUs at all and use an alpha of 0.1 for LeakyReLUs (even though 0.33 is afaik standard) and don't test LeakyReLUs on ImageNet (only ReLUs).

![CIFAR-100](https://raw.githubusercontent.com/aleju/papers/master/neural-nets/images/ELUs__cifar100.png?raw=true "CIFAR-100")

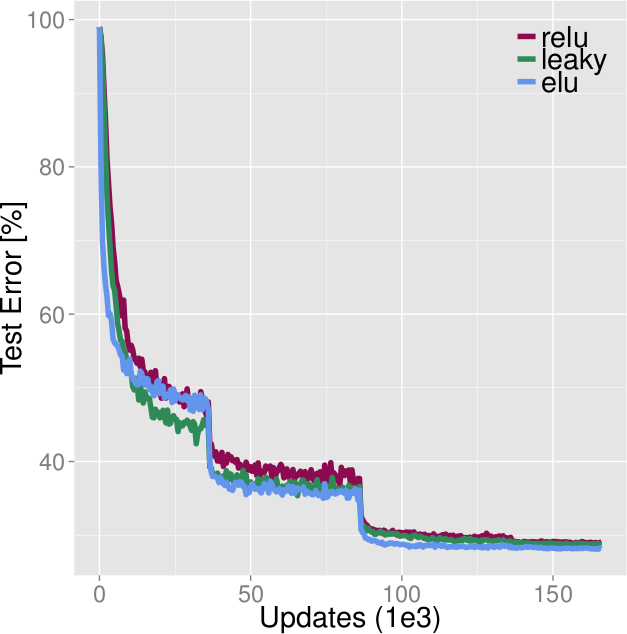
*Comparison of ELUs, LeakyReLUs, ReLUs on CIFAR-100. ELUs ends up with best values, beaten during the early epochs by LeakyReLUs. (Learning rates were optimized for ReLUs.)*

-------------------------

### Rough chapter-wise notes

* Introduction
  * Currently popular choice: ReLUs
  * ReLU: max(0, x)
  * ReLUs are sparse and avoid the vanishing gradient problem, because their derivate is 1 when they are active.
  * ReLUs have a mean activation larger than zero.
  * Non-zero mean activation causes a bias shift in the next layer, especially if multiple of them are correlated.
  * The natural gradient (?) corrects for the bias shift by adjusting the weight update.
  * Having less bias shift would bring the standard gradient closer to the natural gradient, which would lead to faster learning.
  * Suggested solutions:
    * Centering activation functions at zero, which would keep the off-diagonal entries of the Fisher information matrix small.
    * Batch Normalization
    * Projected Natural Gradient Descent (implicitly whitens the activations)
  * These solutions have the problem, that they might end up taking away previous learning steps, which would slow down learning unnecessarily.
  * Chosing a good activation function would be a better solution.
  * Previously, tanh was prefered over sigmoid for that reason (pushed mean towards zero).
  * Recent new activation functions:
    * LeakyReLUs: x if x > 0, else alpha*x
    * PReLUs: Like LeakyReLUs, but alpha is learned
    * RReLUs: Slope of part < 0 is sampled randomly
  * Such activation functions with non-zero slopes for negative values seemed to improve results.
  * The deactivation state of such units is not very robust to noise, can get very negative.
  * They suggest an activation function that can return negative values, but quickly saturates (for negative values, not for positive ones).
  * So the model can make a quantitative assessment for positive statements (there is an amount X of A in the image), but only a qualitative negative one (something indicates that B is not in the image).
  * They argue that this makes their activation function more robust to noise.
  * Their activation function still has activations with a mean close to zero.

* Zero Mean Activations Speed Up Learning
  * Natural Gradient = Update direction which corrects the gradient direction with the Fisher Information Matrix
  * Hessian-Free Optimization techniques use an extended Gauss-Newton approximation of Hessians and therefore can be interpreted as versions of natural gradient descent.
  * Computing the Fisher matrix is too expensive for neural networks.
  * Methods to approximate the Fisher matrix or to perform natural gradient descent have been developed.
  * Natural gradient = inverse(FisherMatrix) * gradientOfWeights
  * Lots of formulas. Apparently first explaining how the natural gradient descent works, then proofing that natural gradient descent can deal well with non-zero-mean activations.
  * Natural gradient descent auto-corrects bias shift (i.e. non-zero-mean activations).
  * If that auto-correction does not exist, oscillations (?) can occur, which slow down learning.
  * Two ways to push means towards zero:
    * Unit zero mean normalization (e.g. Batch Normalization)
    * Activation functions with negative parts

* Exponential Linear Units (ELUs)
  * *Formula*
    * f(x):
      * if x >= 0: x
      * else: alpha(exp(x)-1)
    * f'(x) / Derivative:
      * if x >= 0: 1
      * else: f(x) + alpha
    * `alpha` defines at which negative value the ELU saturates.
    * `alpha=0.5` => minimum value is -0.5 (?)
  * ELUs avoid the vanishing gradient problem, because their positive part is the identity function (like e.g. ReLUs)
  * The negative values of ELUs push the mean activation towards zero.
  * Mean activations closer to zero resemble more the natural gradient, therefore they should speed up learning.
  * ELUs are more noise robust than PReLUs and LeakyReLUs, because their negative values saturate and thus should create a small gradient.
  * "ELUs encode the degree of presence of input concepts, while they do not quantify the degree of absence"

* Experiments Using ELUs
  * They compare ELUs to ReLUs and LeakyReLUs, but not to PReLUs (no explanation why).
  * They seem to use a negative slope of 0.1 for LeakyReLUs, even though 0.33 is standard afaik.
  * They use an alpha of 1.0 for their ELUs (i.e. minimum value is -1.0).
  * MNIST classification:
    * ELUs achieved lower mean activations than ReLU/LeakyReLU
    * ELUs achieved lower cross entropy loss than ReLU/LeakyReLU (and also seemed to learn faster)
    * They used 5 hidden layers of 256 units each (no explanation why so many)
    * (No convolutions)
  * MNIST Autoencoder:
    * ELUs performed consistently best (at different learning rates)
    * Usually ELU > LeakyReLU > ReLU
    * LeakyReLUs not far off, so if they had used a 0.33 value maybe these would have won
  * CIFAR-100 classification:
    * Convolutional network, 11 conv layers
    * LeakyReLUs performed better during the first ~50 epochs, ReLUs mostly on par with ELUs
    * LeakyReLUs about on par for epochs 50-100
    * ELUs win in the end (the learning rates used might not be optimal for ELUs, were designed for ReLUs)
  * CIFER-100, CIFAR-10 (big convnet):
    * 6.55% error on CIFAR-10, 24.28% on CIFAR-100
    * No comparison with ReLUs and LeakyReLUs for same architecture
  * ImageNet
    * Big convnet with spatial pyramid pooling (?) before the fully connected layers
    * Network with ELUs performed better than ReLU network (better score at end, faster learning)
    * Networks were still learning at the end, they didn't run till convergence
    * No comparison to LeakyReLUs