Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks
Denton, Emily L. and Chintala, Soumith and Szlam, Arthur and Fergus, Rob
Neural Information Processing Systems Conference - 2015 via Local Bibsonomy
Keywords: dblp
Denton, Emily L. and Chintala, Soumith and Szlam, Arthur and Fergus, Rob
Neural Information Processing Systems Conference - 2015 via Local Bibsonomy
Keywords: dblp
|
[link]
This post is a comment on the Laplacian pyramid-based generative model proposed by researchers from NYU/Facebook AI Research.
Let me start by saying that I really like this model, and I think - looking at the samples drawn - it represents a nice big step towards convincing generative models of natural images.
To summarise the model, the authors use the Laplacian pyramid representation of images, where you recursively decompose the image to a lower resolution subsampled component and the high-frequency residual. The reason this decomposition is favoured in image processing is the fact that the high-frequency residuals tend to be very sparse, so they are relatively easy to compress and encode.
In this paper the authors propose using convolutional neural networks at each layer of the Laplacian pyramid representation to generate an image sequentially, increasing the resolution at each step. The convnet at each layer is conditioned on the lower resolution image, and some noise component $z_k$, and generates a random higher resolution image. The process continues recursively until the desired resilution is reached. For training they use the adversarial objective function. Below is the main figure that explains how the generative model works, I encourage everyone to have a look at the paper for more details:
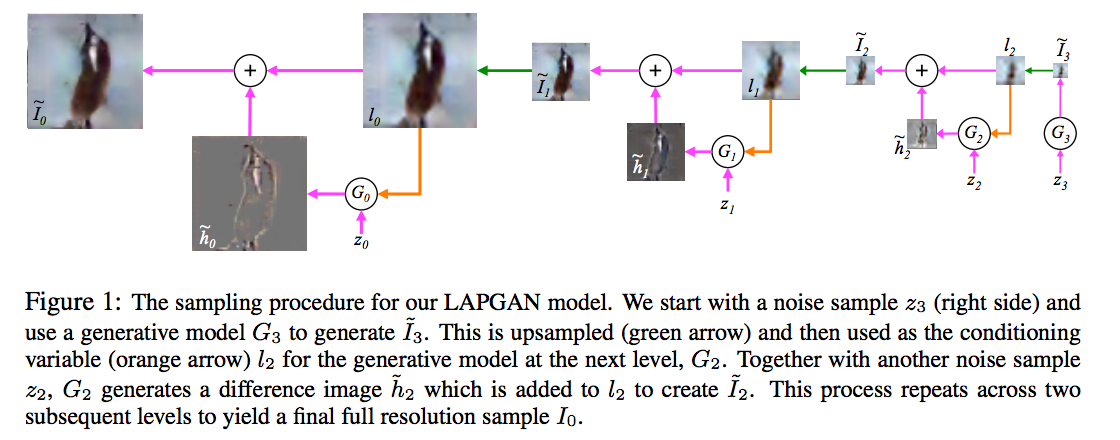
#### An argument about Conditional Entropies
What I think is weird about the model is the precise amount of noise that is injected at each layer/resolution. In the schematic above, these are the $z_k$ variables. Adding the noise is crucial to defining a probabilistic generative process; this is how it defines a probability distribution.
I think it's useful to think about entropies of natural images at different resolutions. When doing generative modelling or unsuperised learning, we want to capture the distribution of data. One important aspect of a probability distribution is its entropy, which measures the variability of the random quantity. In this case, we want to describe the statistics of the full resolution observed natural image $I_0$. (I borrow the authors' notation where $I_0$ represents the highest resolution image, and $I_k$ represent the $k$-times subsampled version. Using the Laplacian pyramid representation, we can decompose the entropy of an image in the following way:
$$\mathbb{H}[I_0] = \mathbb{H}[I_{K}] + \sum_{k=0}^{K-1} \mathbb{H}[I_k\vert I_{k+1}].$$
The reason why the above decomposition holds is very simple. Because $I_{k+1}$ is a deterministic function of $I_{k}$ (subsampling), the conditional entropy $\mathbb{H}[I_{k+1}\vert I_{k}] = 0$. Therefore the joint entropy of the two variables is simply the entropy of the higher resolution image $I_{k}$, that is $\mathbb{H}[I_{k},I_{k+1}] = \mathbb{H}[I_{k}] + \mathbb{H}[I_{k+1}\vert I_{k}] = \mathbb{H}[I_{k}]$. So by induction, the join entropy of all images $I_{k}$ is just the marginal entropy of the highest resolution image $I_0$. Applying the chain rule for joint entropies we get the expression above.
Now, the interesting bit is how the conditional entropies $\mathbb{H}[I_k\vert I_{k+1}]$ are 'achieved' in the Laplacian pyramid generative model paper. These entropies are provided by the injected random noise variables $z_k$. By the information processing lemma $\mathbb{H}[I_k\vert I_{k+1}] \leq \mathbb{H}[z_k]$. The authors choose $z_k$ to be uniform random variables whose dimensionality grows with the resolution of $I_k$. To quote them "The noise input $z_k$ to $G_k$ is presented as a 4th color plane to low-pass $l_k$, hence its dimensionality varies with the pyramid level." Therefore $\mathbb{H}[z_k] \propto 4^{-k}$, assuming that the pixel count quadruples at each layer.
So the conditional entropy $\mathbb{H}[I_k\vert I_{k+1}]$ is allowed to grow exponentially with resolution, at the same rate it would grow if the images contained pure white noise. In their model, they allow the per-pixel conditional entropy $c\cdot 4^{-k}\cdot \mathbb{H}[I_k\vert I_{k+1}]$ to be constant across resolutions. To me, this seems undesirable. My intuition is, for natural images, $\mathbb{H}[I_k\vert I_{k+1}]$ may grow as $k$ decreases (because the dimensionality gorws), but the per-pixel value $c\cdot 4^{k}\cdot \mathbb{H}[I_k\vert I_{k+1}]$ should decrease or converge to $0$ as the resolution increases. Very low low-resolution subsampled natural images behave a little bit like white noise, there is a lot of variability in them. But as you increase the resolution, the probability distribution of the high-res image given the low-res image will become a lot sharper.
In terms of model capacity, this is not a problem, inasmuch as the convolutional models $G_{k}$ can choose to ignore some variance in $z_k$ and learn a more deterministic superresolution process. However, adding unnecessarily high entropy will almost certainly make the fitting of such model harder. For example, the adversarial training process relies on sampling from $z_k$, and the procedure is pretty sensitive to sampling noise. If you make the distribution of $z_k$ unneccessarily high entropy, you will end up doing a lot of extra work during training until the network figures out to ignore the extra variance.
To solve this problem, I propose to keep the entropy of the noise vectors constant, or make them grow sub-linearly with the number of pixels in the image. This mperhaps akes the generative convnets harder to implement. Another quick solution would be to introduce dependence between components of $z_k$ via a low-rank covariance matrix, or some sort of a hashing trick.
#### Adversarial training vs superresolution autoencoders
Another weird thing is that the adversarial objective function forgets the identity of the image. For example, you would want your model so that
`"if at the previous layer you have a low-resolution parrot, the next layer should be a higher-resolution parrot"`
Instead, what you get with the adversarial objective is
`"if at the previous layer you have a low-resolution parrot, the next layer should output a higher-dimensional image that looks like a plausible natural image"`
So, there is nothing in the objective function that enforces dependency between subsequent layers of the pyramid. I think if you made $G_k$ very complex, it could just learn to model natural images by itself, so that $I_{k}$ is in essence independent of $I_{k+1}$ and is purely driven by the noise $z_{k}$. You could sidestep this problem by restricting the complexity of the generative nets, or, again, to restrict the entropy of the noise.
Overall, I think the approach would benefit from a combination of the adversarial and a supervised (superresolution autoencoder) objective function.

Your comment:
|
You must log in before you can submit this summary! Your draft will not be saved!
Preview:












