inFERENCe

I spend the week at ICML, and this paper on generative models is one of my favourites so far:

To be clear: this post doesn't add much to the presentation of the paper, but I will attempt to summarise my understanding of it. Also, I want to make clear that this is not my work.

Unsupervised learning has been one of the most interesting areas of machine learning in the last decades, but it is in the spotlight again since the deep learning crowd started to care about it. Unsupervised learning is hard because evaluating the loss function people want to use (log likelihood) is intractable for most interesting models. Therefore people come up with

- alternative objective functions, such as adversarial training, maximum mean discrepancy, or pseudolikelihood, which can be evaluated for a large class of interesting models
- alternative optimisation methods or approximate inference methods such as contrastive divergence or variational Bayes
- models that have some nice properties. This paper is an example of the latter

#### The key idea behind the paper

What we typically try to do in representation learning is to map data to a latent representation. While the Data can have arbitrarily complex distribution along some complicated nonlinear manifold, we want the computed latent representations to have a nice distribution, like a multivariate Gaussian.

This paper takes this idea very explicitly using a stochastic mapping to turn data into a representation: a random diffusion process. If you take any data, and apply Brownian motion-like stochastic process to this, you will end up with a standard Gaussian distributed variable, due to the stationarity of the Brownian motion. Below image shows an example: 2D observations (left) have a complex data distribution along the Swiss roll manifold. If one applies Brownian motion to each datapoint, the complicated structure starts to diffuse, and eventually the data is scrambled to become white noise (right).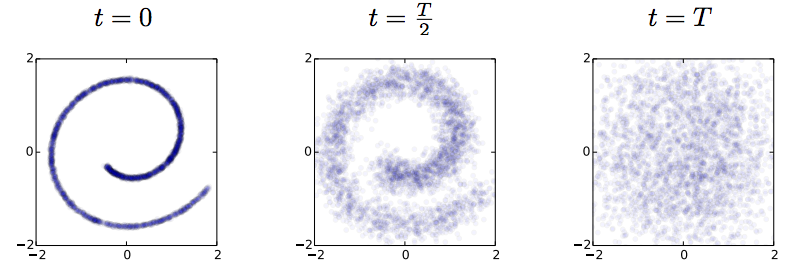

![](http://www.inference.vc/content/images/2015/07/Screen-Shot-2015-07-09-at-13-27-41.png)

Now the trick the authors used is to train a dynamical system to inverts this random walk, to be able to reconstruct the original data distribution from the random Gaussian noise. Amazingly, this works, and the traninig objective becomes very similar to variational autoencoders. Below is a figure showing what happens when we try to reconstruct data in the Swiss roll example: The top images from right to left: we start with a bunch of points drawn from random noise (top right). We apply the inverse nonlinear transformation to these points (top middle). Over time points will be pushed towards the original Swiss roll manifold (top left).

`The information about the data distribution is encoded in the approximate inverse dynamical system`

The bottom pictures show where this dynamical system tries to push points as time progresses.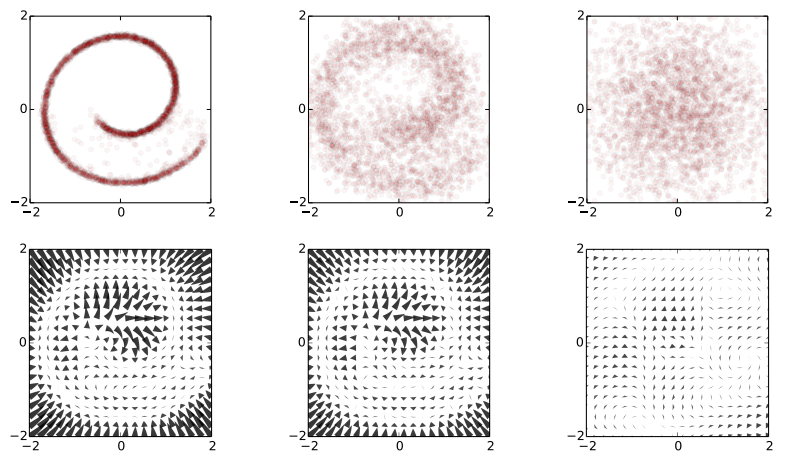

![](http://www.inference.vc/content/images/2015/07/Screen-Shot-2015-07-09-at-13-30-16.png)

This is super cool. Now we have a deep generative process that can turn random noise into something that looks like our datapoints. It can generate roughly natural-looking images like these:

![](http://www.inference.vc/content/images/2015/07/Screen-Shot-2015-07-09-at-13-33-38.png)

 #### Advantages

In this model a lot of things that are otherwise hard to do are easy to do:

1. generating/imagining data is straightforward
2. inference, i.e. calculating the latent representation from data, is simple
3. you can multiply the distribution with another distribution, making Bayesian calculations for stuff like denoising or superresolution possible.

#### Drawbacks and extensions

I think a drawback of the model is that if you run the diffusion process for too long (i.e. make the model deeper), the mutual information between datapoint and its representation is bound to decrease, due to the stationarity of Brownian motion. I guess this is going to be an important limitation to the depth of these models.

Also, the latent representations at each layer are assumed to be exactly if the same dimensionality and type as the data itsef. So if we are modeling 100x100 images, then all layers in the resulting network will have 100k nodes. I guess this can be overcome by combining variational autoencoders with this method. Also, you can imagine augmenting your space with extra 'pixels' that are only used for richer representations in the intermediate layers.

Anyway, this is super cool, go read the paper.

This is my second favourite paper from ICML last week, and I think the title really does not do it justice. It is a great idea about training rich, tractable autoregressive generative models of data, and doing so by using standard techniques from autoencoder training with dropout.

Caveat (again): this is not my work, and this blog post does not really add anything new to the paper, only my perspective on it.

#### Unsupervised learning primer (again)

Unsupervised learning is about modelling the probability distribution $p(\mathbf{x})$ of some data, from which we observe independent samples $\mathbf{x}_i$. Often, the vector $\mathbf{x}$ is high dimensional, such as in images, where different components of $\mathbf{x}$ encode pixel intensities.

Typically, a probability model is specified as $q(\mathbf{x};\theta) = \frac{f(\mathbf{x};\theta)}{Z_\theta}$, where $f(\mathbf{x};\theta)$ is some positive function parametrised by $\theta$. The denominator $Z_\theta$ is called the normalisation constant which makes sure that $q$ is a valid probability model: it has to sum up to one over all possible configurations of $\mathbf{x}$. The central problem in unsupervised learning is that for the most interesting models in high dimensional spaces, calculating $Z_\theta$ is intractable, so crucial quantities such as the model likelihood cannot be calculated and the model cannot be fitted. The community is therefore in search for

- interesting models that have tractable normalisation constants
- fancy methods to deal with intractable models (pseudo-likelihood, adversarial networks, contrastive divergence)

This paper is about the former.

#### Core ingredient: autoregressive models

This paper sidesteps the high dimensional normalisation problem by restricting the class of probability distributions to autoregressive models, which can be written as follows:

$$q(\mathbf{x};\theta) = \prod_{d=1}^{D} q(x_{d}\vert x_{1:d-1};\theta).$$

Here $x_d$ denotes the $d^{th}$ component of the input vector $\mathbf{x}$. In a model like this, we only need to compute the normalisation of each $q(x_{d}\vert x_{1:d-1};\theta)$ term, and we can be sure that the resulting model is a valid model over the whole vector $\mathbf{x}$. But as normalising these one-dimensional probability distributions is a lot easier, we have a whole range of interesting tractable distributions at our disposal.

#### Training multiple models simultaneously

Autoregressive models are used a lot in time series modelling and language modelling: hidden Markov models or recurrent neural networks are examples. There, autoregressive models are a very natural way to model data because the data comes ordered (in time).

What's weird about using autoregressive models in this context is that it is sensitive to ordering of dimensions, even though that ordering might not mean anything. If $\mathbf{x}$ encodes an image, you can think about multiple orders in which pixel values can be serialised: sweeping left-to-right, top-to-bottom, inside-out etc. For images, neither of these orderings is particularly natural, yet all of these different ordering specifies a different model above.

But it turns out, you don't have to choose one ordering, you can choose all of them at the same time. The neat trick in the masking autoencoder paper is to train multiple autoregressive models all at the same time, all of them sharing (a subset of) parameters $\theta$, but defined over different ordering of coordinates. This can be achieved by thinking of deep autoregressive models as a special cases of an autoencoder, only with a few edges missing.

![](http://www.inference.vc/content/images/2015/07/Screen-Shot-2015-07-13-at-10-48-54.png)

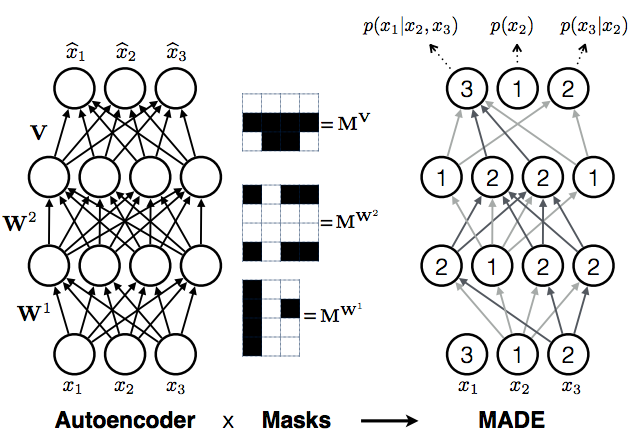
Consider a fixed ordering of input dimensions. Now take a fully connected autoencoder, which defines a probability distribution $q(\hat{\mathbf{x}}\vert\mathbf{x};\theta)$. You can write this as

$$q(\hat{\mathbf{x}}\vert\mathbf{x};\theta) = \prod_{d=1}^{D} q(\hat{x}_{d}\vert x_{1:D};\theta)$$

Note the similarity to the autoregressive equation above, the only difference being that each coordinate now depends on every other coordinate ($x_{1:D}$), rather than only coordinates that precede it in the ordering ($x_{1:d-1}$). To turn this equation into autoregressive equation above, we simply have to remove dependencies of each output coordinate $\hat{x}_{d}$ on any input coordinate $\hat{x}_{e}$, where $e>=d$. This can be done by removing edges along all paths from the input coordinate $\hat{x}_{e}$ to output coordinate $\hat{x}_{d}$. You can achieve this cutting of edges by multiplying the weight matrices $\mathbf{W}^{l}$of the autoencoder neural network elementwise by binary masking matrices $\mathbf{M}^{\mathbf{W}^{l}}$. Hence the name masked autoencoder.

The procedure above considered a fixed ordering of coordinates. You can repeat this process for any arbitrary ordering, for which you obtain different masking matrices but otherwise the same procedure. If you train this autoencoder network with randomly sampled masking matrices, you essentially train a family of autoregressive models, each sharing some parameters via the underlying autoencoder network.

Because masking is similar to the popular dropout training, implementing it is relatively straightforward and requires minimal change to existing autoencoder code. However, now you have a generative model - in fact, a large set of generative models - which has a lot of nice properties for you to enjoy.

The slight concern

Of course, this would be all too good to be true: a powerful deep generative model that is easy to evaluate and all. I think the problem with this is the following: If you train just one of these autoregressive models, that's tractable, exact and fine. But you really want to combine all (or many) of these becuause individually they are weak.

What is the interpretation of training with randomly drawn masking matrices? You can think of it as stochastic gradient descent on the following objective:

$$\mathbb{E}_{\mathbf{x}\sim p}\mathbb{E}_{\pi \sim U} \log q(\mathbf{x},\pi,\theta)$$

Here, I used $\pi$ to denote a permutation of the coordinates, and $\mathbb{E}_{\pi \sim U}$ to take an expectation over a uniform distribution over permutations. The distribution $q(\mathbf{x},\pi,\theta)$ is the autoregressive model defined by $\theta$ and the masking matrices corresponding to permutation $\pi$. $\mathbb{E}_{\mathbf{x}\sim p}$ denotes averaging over the empirical data distribution.

Combining as a mixture model

One way to combine autoregressive models is to take a mixture model. In the paper, the authors actually use an ensemble to make predictions, which is analogous to an equal mixture model where the mixture weights are uniform and fixed. The likelihood for this model would be the following:

$$\mathbb{E}_{\mathbf{x}\sim p} \log \mathbb{E}_{\pi \sim U} q(\mathbf{x},\pi,\theta)$$

Notice that the averaging over permutations now takes place inside the logarithm. By Jensen's inequality, we can say that randomly sampling masking matrices during training amounts to optimising a stochastically estimated lower bound to the likelihood of an equal mixture. This raises the question whether actually learning the weights in such a model would be hard using something like an EM algorithm with a sparsity-enforcing regulariser/prior over mixture weights.

Combining as a product of experts model

Combining these autoregressive models as a mixture is not ideal. In mixture modeling the sharpness of the mixture distribution is bounded by the sharpness of component distributions. Your combined prediction can never be more confident than the your most confident model. In this case, I expect the AR models to be pretty poor models individually, and therefore not to be very sharp, particularly along the first few coordinates in the corresponding ordering.

A better way to combine probabilistic models is via product of experts. You can actually interpret training by random masking matrices as a form of product of experts, but with the global normalisation ignored. I'm not sure if it would be possible/tractable to do anything better than this.

This post is a comment on the Laplacian pyramid-based generative model proposed by researchers from NYU/Facebook AI Research.

Let me start by saying that I really like this model, and I think - looking at the samples drawn - it represents a nice big step towards convincing generative models of natural images.

To summarise the model, the authors use the Laplacian pyramid representation of images, where you recursively decompose the image to a lower resolution subsampled component and the high-frequency residual. The reason this decomposition is favoured in image processing is the fact that the high-frequency residuals tend to be very sparse, so they are relatively easy to compress and encode.

In this paper the authors propose using convolutional neural networks at each layer of the Laplacian pyramid representation to generate an image sequentially, increasing the resolution at each step. The convnet at each layer is conditioned on the lower resolution image, and some noise component $z_k$, and generates a random higher resolution image. The process continues recursively until the desired resilution is reached. For training they use the adversarial objective function. Below is the main figure that explains how the generative model works, I encourage everyone to have a look at the paper for more details:

![](http://www.inference.vc/content/images/2015/07/Screen-Shot-2015-07-23-at-11-15-17.png)

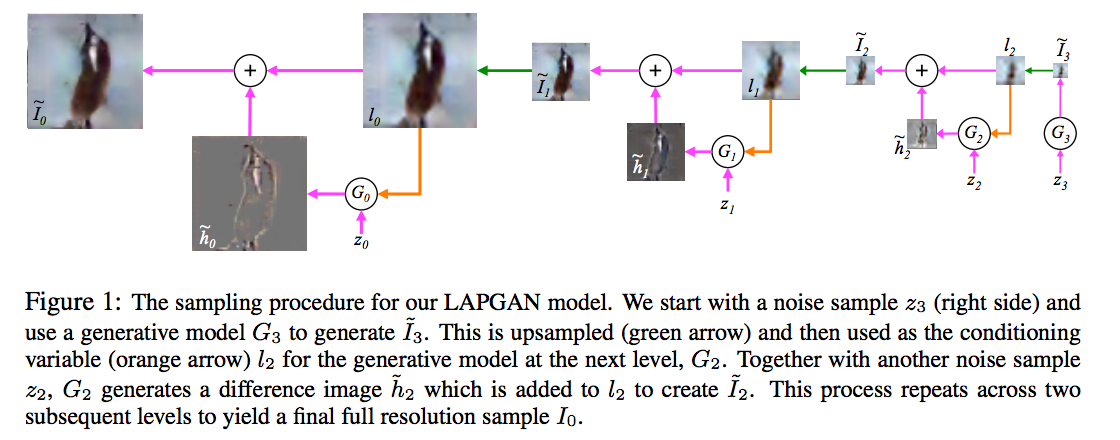
#### An argument about Conditional Entropies

What I think is weird about the model is the precise amount of noise that is injected at each layer/resolution. In the schematic above, these are the $z_k$ variables. Adding the noise is crucial to defining a probabilistic generative process; this is how it defines a probability distribution.

I think it's useful to think about entropies of natural images at different resolutions. When doing generative modelling or unsuperised learning, we want to capture the distribution of data. One important aspect of a probability distribution is its entropy, which measures the variability of the random quantity. In this case, we want to describe the statistics of the full resolution observed natural image $I_0$. (I borrow the authors' notation where $I_0$ represents the highest resolution image, and $I_k$ represent the $k$-times subsampled version. Using the Laplacian pyramid representation, we can decompose the entropy of an image in the following way:

$$\mathbb{H}[I_0] = \mathbb{H}[I_{K}] + \sum_{k=0}^{K-1} \mathbb{H}[I_k\vert I_{k+1}].$$

The reason why the above decomposition holds is very simple. Because $I_{k+1}$ is a deterministic function of $I_{k}$ (subsampling), the conditional entropy $\mathbb{H}[I_{k+1}\vert I_{k}] = 0$. Therefore the joint entropy of the two variables is simply the entropy of the higher resolution image $I_{k}$, that is $\mathbb{H}[I_{k},I_{k+1}] = \mathbb{H}[I_{k}] + \mathbb{H}[I_{k+1}\vert I_{k}] = \mathbb{H}[I_{k}]$. So by induction, the join entropy of all images $I_{k}$ is just the marginal entropy of the highest resolution image $I_0$. Applying the chain rule for joint entropies we get the expression above.

Now, the interesting bit is how the conditional entropies $\mathbb{H}[I_k\vert I_{k+1}]$ are 'achieved' in the Laplacian pyramid generative model paper. These entropies are provided by the injected random noise variables $z_k$. By the information processing lemma $\mathbb{H}[I_k\vert I_{k+1}] \leq \mathbb{H}[z_k]$. The authors choose $z_k$ to be uniform random variables whose dimensionality grows with the resolution of $I_k$. To quote them "The noise input $z_k$ to $G_k$ is presented as a 4th color plane to low-pass $l_k$, hence its dimensionality varies with the pyramid level." Therefore $\mathbb{H}[z_k] \propto 4^{-k}$, assuming that the pixel count quadruples at each layer.

So the conditional entropy $\mathbb{H}[I_k\vert I_{k+1}]$ is allowed to grow exponentially with resolution, at the same rate it would grow if the images contained pure white noise. In their model, they allow the per-pixel conditional entropy $c\cdot 4^{-k}\cdot \mathbb{H}[I_k\vert I_{k+1}]$ to be constant across resolutions. To me, this seems undesirable. My intuition is, for natural images, $\mathbb{H}[I_k\vert I_{k+1}]$ may grow as $k$ decreases (because the dimensionality gorws), but the per-pixel value $c\cdot 4^{k}\cdot \mathbb{H}[I_k\vert I_{k+1}]$ should decrease or converge to $0$ as the resolution increases. Very low low-resolution subsampled natural images behave a little bit like white noise, there is a lot of variability in them. But as you increase the resolution, the probability distribution of the high-res image given the low-res image will become a lot sharper.

In terms of model capacity, this is not a problem, inasmuch as the convolutional models $G_{k}$ can choose to ignore some variance in $z_k$ and learn a more deterministic superresolution process. However, adding unnecessarily high entropy will almost certainly make the fitting of such model harder. For example, the adversarial training process relies on sampling from $z_k$, and the procedure is pretty sensitive to sampling noise. If you make the distribution of $z_k$ unneccessarily high entropy, you will end up doing a lot of extra work during training until the network figures out to ignore the extra variance.

To solve this problem, I propose to keep the entropy of the noise vectors constant, or make them grow sub-linearly with the number of pixels in the image. This mperhaps akes the generative convnets harder to implement. Another quick solution would be to introduce dependence between components of $z_k$ via a low-rank covariance matrix, or some sort of a hashing trick.

#### Adversarial training vs superresolution autoencoders

Another weird thing is that the adversarial objective function forgets the identity of the image. For example, you would want your model so that

`"if at the previous layer you have a low-resolution parrot, the next layer should be a higher-resolution parrot"`

Instead, what you get with the adversarial objective is

`"if at the previous layer you have a low-resolution parrot, the next layer should output a higher-dimensional image that looks like a plausible natural image"`

So, there is nothing in the objective function that enforces dependency between subsequent layers of the pyramid. I think if you made $G_k$ very complex, it could just learn to model natural images by itself, so that $I_{k}$ is in essence independent of $I_{k+1}$ and is purely driven by the noise $z_{k}$. You could sidestep this problem by restricting the complexity of the generative nets, or, again, to restrict the entropy of the noise.

Overall, I think the approach would benefit from a combination of the adversarial and a supervised (superresolution autoencoder) objective function.

I think this paper has two main ideas in there, I see them as independent, for reasons explained below:

- A new penalty function that aims at regularising the second derivative of the trajectory the latent representation traces over time. I see this as a generalisation of the slowness principle or temporal constancy, more about this in the next section.

- A new autoencoder-like method to predict future frames in video. Video is really hard to forward-predict with non-probabilistic models because high level aspects of video are genuinely uncertain. For example, in a football game, you can't really predict whether the ball will hit the goalpost, but the results might look completely different visually. This, combined with L2 penalties often results in overly conservative, blurry predictions. The paper improves things by introducing extra hidden variables, that allow the model to represent uncertainty in its predictions. More on this later.

#### Inductive bias: penalising curvature

The key idea of this paper is to learn good distributed representations of natural images from video in an unsupervised way. Intuitively, there is a lot of information contained in video, which is lost if you scramble the video and look at statistics individual frames only. The race is on to develop the right kind of prior and inductive bias that helps us fully exploit this temporal information. This paper presents a way, which is called learning to linearise (I'm going to call this L2L).

Naturally occurring images are thought to reside on some complex, nonlinear manifold whose intrinsic dimension is substantially lower than the number of pixels in an image. It is then natural to think about video as a journey on this manifold surface, along some smooth path. Therefore, if we aim to learn good generic features that correspond to coordinates on this underlying manifold, we should expect that these features vary in a smooth fashion over time as you play the video.

L2L uses this intuition to motivate their choice of an objective function that penalises a scale-invariant measure of curvature over time. In a way it tries to recover features that transform nearly linearly as time progresses and the video is played.

In their notations, $x_{t}$ denotes the data in frame $t$, which is transformed by a deep network to obtain the latent representation $z_{t}$. The penalty for the latent representation is as follows.

$$-\sum_{t} \frac{(z_t - z_{t-1})^{T}(z_{t+1} - z_{t})}{\|z_t - z_{t-1}\|\|z_{t+1} - z_{t}\|}$$

The expression above has a geometric meaning as the cosine of the angle between the vectors $(z_t - z_{t-1})$ and $(z_{t+1} - z_{t})$. The penalty is minimised if these two vectors are parallel and point in the same direction. In other words the penalty prefers when the latent feature representation keeps its momentum and continues along a linear path - and it does not like sharp turns or jumps. This seems like a sensible prior assumption to build on.

L2L is very similar to another popular inductive bias used in slow feature analysis: the temporal slowness principle. According to this principle, the most relevant underlying features don't change very quickly. The slowness principle has a long history both in machine learning and as a model of human visual perception. In SFA one would minimise the following penalty on the latent representation:

$$\sum_{t} (z_t - z_{t-1})^{2},$$

where the square is applied component-wise. There are additional constraints in SFA, more about this later. We can understand the connection between SFA and this paper's penalty if we plot the penalty for a single hidden feature $z_{t,f}$ at time $t$, keeping all other features and values at neighbouring timesteps constant. This is plotted in the figure below (scaled and translated so the objectives line up nicely).

![](http://www.inference.vc/content/images/2015/09/-RfX4Dp2Y3YAAAAASUVORK5CYII-.png)

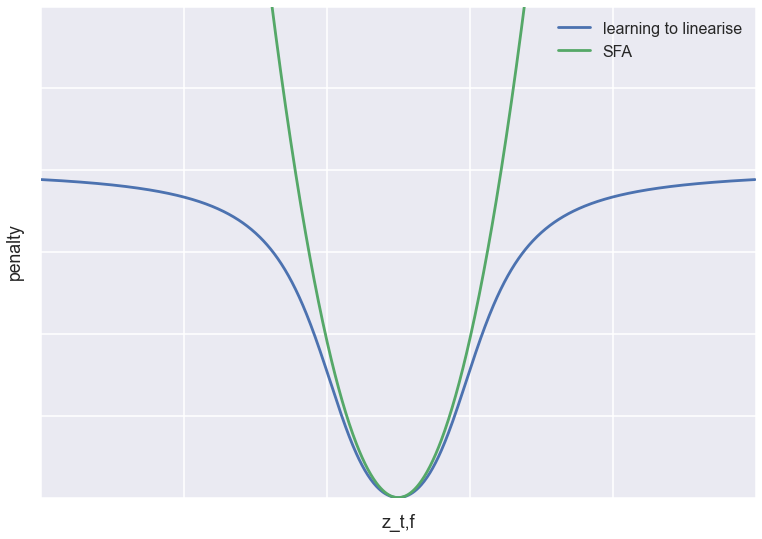
As you can see, both objectives have a minimum at the same location: they both try to force $z_{t,f}$ to linearly interpolate between the neighbouring timesteps. However, while SFA has a quadratic penalty, the learning to linearise objective tapers off at long distances. Compare this to Tukey's loss function used in outlier-resistant robust regression.

Based on this, my prediction is that compared to SFA, this loss function is more tolerant of outliers, which in the temporal domain would mean abrupt jumps in the latent representation. So while SFA is equivalent to assuming that the latent features follow a Brownian-motion-like Ornstein–Uhlenbeck process, I'd imagine this prior corresponds to something like a jump diffusion process (although I don't think the analogy holds mathematically).

Which one of these inductive biases/priors are better at exploiting temporal information in natural video? Slow Brownian motion, or nearly-linear trajectories with potentially a few jumps Unfortunately, don't expect any empirical answer to that from the paper. All experiments seem to be performed on artificially constructed examples, where the temporal information is synthetically engineered. Nor there is any real comparison to SFA.

#### Representing predictive uncertainty with auxillary variables

While the encoder network learns to construct smoothly varrying features $z_t$, the model also has a decoder network that tries to reconstruct $x_t$ and predict subsequent frames. This, the authors agree, is necessary in order for $z_t$ to contain enough relevant information about the frame $x_t$ (more about whether or not this is necessary later). The precise way this decoding is done has a novel idea as well: minimising over auxillary variables.

Let's say our task is to predict a future frame $x_{t+k}$ based on the latent representation $z_{t}$. The problem is, this is a very hard problem. In video, just like in real life, anything can happen. Imagine you're modelling soccer footage, and the ball is about to hit the goalpost. In order to predict the next frames, not only do we have to know about natural image statistics, we also have to be able to predict whether the goal is in or not. An optimal predictive model would give a highly multimodal probability distribution as its answer. If you use the L2 loss with a deterministic feed-forward predictive network, it's likely to come up with a very blurry image, which would correspont to the average of this nasty multimodal distribution. This calls for something better, either a smarter objective function, or a better way of representing predictive uncertainty.

The solution the authors gave is to introduce hidden variables $\delta_{t}$, that the decoder network also receives as input in addition to $z_t$. For each frame, $\delta_t$ is optimised so that only the best possible reconstruction is taken into account in the loss function. Thus, the decoder network is allowed to use $\delta$ as a source of non-determinism to hedge its bets as to what the contents of the next frame will be. This is one step closer to the ideal setting where the decoder network is allowed to give a full probability distribution of possibilities and then is evaluated using a strictly proper scoring rule.

This inner loop minimisation (of $\delta$) looks very tedious, and introduces a few more parameters that may be hard to set. The algorithm is reminiscent of the E-step in expectation-maximisation, and also very similar to the iterated closest point algorithm Andrew Fitzgibbon talked about in his tutorial at BMVC this year.

In his tutorial, Andrew gave examples where jointly optimising model parameters and auxiliary variables ($\delta$) is advantageous, and I think the same logic applies here. Instead of the inner loop, simultaneous optimisation helps fixing some pathologies, like slow convergence near the optimum. In addition, Andrew advocates exploiting the sparsity structure of the Hessian to implement efficient second-order gradient-based optimisation methods. These tricks are explained in paragraphs around equation 8 in (Prasad et al, 2010).

#### Predictive model: Is it necessary?

On a more fundamental level, I question whether the predictive decoder network is really a necessary addition to make L2L work.

The authors observe that the objective function is minimised by the "trivial" solutions $z_{t} = at + b$, where $a,b$ can be arbitrary constants. They then say that in order to make sure features do something more than just discover some of these trivial solutions, we also have to include a decoder network, that uses $z_t$ to predict future frames. I believe this is not necessary at all.

Because $z_t$ is a deterministic function of $x_t$, and $t$ is not accessible to $z_{t}$ in any other way than through inferring it from $x_t$, as long as $a\neq 0$, the linear solutions are not trivial at all. If the network discovers $z_{t} = at, a\neq 0$, you should in fact be very happy (assuming a single feature). The only problems with trivial solutions occur when $z_{t} = b$ ($z$ doesn't depend on the data at all) or when $z$ is multidimensional and several redundant features are sensitive to exactly the same thing.

These trivial solutions could be avoided the same way they are avoided in SFA, by constraining the overall spatial covariance of $z_{t}$ over the videoclip to be $I$. This would force each feature to vary at least a little bit with data- hence avoiding the trivial constant solutions. It would also force features to be linearly decorrelated - solving the redundant features problem.

So I wonder if the decoder network is indeed a necessary addition to the model. I would love to encourage the authors to implement their new hypothesis of a prior both with and without the decoder. They may already have tried it without and found it really didn’t work, so it might just be a matter of including those results. This would in turn allow us to see SFA and L2L side-by-side, and learn something about whether and why their prior is better than the sl

Google's team developed scheduled sampling as an alternative training procedure to fit RNNs, and they used it in their competition-winning method for image captioning. While I can't argue with the empirical results (so I won't), I was a bit skeptical about the technique at a fundamental level, so I decided to do a bit of math that resulted in this blog post.

Overall, I have a suspicion that scheduled sampling is a flawed objective function for unsupervised/generative modelling, and I want to use this post to explain why I think so. I hope the comments section will work this time so people can comment and argue otherwise. Please also shoot me an email if you have more to say.

#### Summary of this note

- I have a critical look at scheduled sampling as objective function for training RNNs
- I show it can lead to pathologies where the RNN learns marginal instead of conditional distributions
- I explain why I think adversarial training/generative moment matching offers a better alternative
- Lastly, I include a paragraph in which I apologise for being a di*k again.

#### Strictly proper scoring rules

I've mentioned scoring rules on this blog many times, and my PhD thesis was about them, so saying I'm obsessed with this topic would be a valid observation. But this is important stuff, particularly for unsupervised learning, and particularly as a framework to think about hard concepts like overfitting in generative models.

Scoring rules are essentially loss functions for probabilistic models/forecasts. A scoring rule $$S(x,Q)$$ simply measures how bad a probabilistic forecast $Q$ for a variable is in the light of actual observation $x$. In this notation, lower is better. A scoring rule is called strictly proper, if for any $P$, the following holds:

$$\underset{Q}{\operatorname{argmax}} \mathbb{E}_{x\sim P}S(x,Q) = P$$

In other words, if you repeatedly sample observations from some true underlying distribution $P$, then the model $Q$ which minimises expected score is $P$. This means that the scoring rule cannot be fooled and that minimising the expected score yields a consistent estimator for $P$. Because I mention consistency, people may dismiss this as a learning theory argument, but it is not. If you are a Bayesian or a deep learning person with no interest in consistency, a scoring rule being strictly proper simply means that it is safe to use it as a loss function. Anything that's not strictly proper is weird and wrong, it will lead to learning the wrong thing.

This concept is central in unsupervised learning and generative modelling. Unsupervised learning is all about modelling the probability distribution of data, so it's essential that we have loss functions that can measure the discrepancy between our model $Q$, and the true data distribution $P$ in a consistent way.

#### log-likelihood

One of the most frequently used strictly proper scoring rule is the logarithmic score:

$$S(x,Q) = - \log Q(x)$$

This quantity is also known as the negative log-likelihood. Minimising the expected score in an i.i.d scenario yields maximum likelihood estimation, which is known to be a consistent estimator and has nice properties.

Often, the likelihood is impossible to evaluate. Luckily, it is not the only strictly proper scoring rule. In the context of generative models people have used the pseudolikelihood, score matching and moment matching, all of which are examples of strictly proper scoring rules.

To recap, any learning method that corresponds to minimising a strictly proper scoring rule is fine, everything else can go horribly wrong, even if we feed it infinite data, it might just learn the wrong thing.

#### Scheduled Sampling

After successfully establishing myself as a proper-scoring-rule-nazi, let's talk about scheduled sampling (SS). I don't have a lot of space explaining SS in great detail here, only the basic idea. I encourage everyone to read the paper and Hugo's summary above.

SS is a new method to train recurrent neural networks(RNNs) to model sequences. I will use character-by-character models of text as an example. Typically, when you train an RNN, you aim to minimise the log predictive likelihood in predicting the next character in each training sentence, given the prefix string of previous characters. This can be thought of as a special case of maximum likelihood learning, and is all fine, you can actually do this properly without approximations.

After training, you use the RNN to generate sample sentences in a recursive fashion: assuming you've already generated $n$ characters, you feed that prefix into the RNN, and ask it to predict the $n+1$st character. The $n+1$st character is then added to the prefix to predict the $n+2$th character, and so on.

The authors say there is a disconnect between how the model is trained (it's always fed real data) and how it's used (it's always fed synthetic data generated by itself). This, they argue, leads to the RNN being unable to recover from its own mistakes early on in the sentence.

To address this, the authors propose an alternative training strategy, where every once in a while, the network is given its own synthetic data instead of real data at training time. More specifically, for each character in the training sentences, we flip a coin to decide whether we feed the character from the real training sentence, or whether to feed the model's own prediction as to what that character would have been. The authors claim this makes the model more robust to recovering from mistakes, which is probably true.

As far as I'm concerned, I'm happy as long as the new training procedure corresponds to a strictly proper scoring rule. But in this case, I have a strong feeling that it does not.

#### case study: sequence of two variables

For sake of simplicity, let's consider using scheduled sampling to learn the joint distribution of a sequence of just two random variables. This is probably the simplest (shortest) time series I can think of. So SS in this case works as follows: For each datapoint train the network to predict the real $x_1$. Then we flip a coin to decide whether to keep $x_1$ from the datapoint, or to replace it with a sample from the model $Q_{x_1}$. Then we train $Q_{x_2\vert x_1}$ on the $(x_1,x_2)$ pair obtained this way.

The scoring rule for selective sampling looks something like this:

$$ S(Q_{x_1,x_2},(x_1,x_2)) = - (1 - \epsilon) [ \mathbb{E}_{z \sim Q_{x_1}} \log Q_{x_2 \vert x_1}(x_2 \vert z) + \log Q_{x_1}(x_1)] - \epsilon \log Q_{x_2 , x_1}(x_1,x_2),$$

where $\epsilon$ is the probability with wich the true $x_1$ is used.

The authors suggest starting training with $\epsilon=1$ and annealing it so that by the end of the training $\epsilon=0$. So as far as the eventual optimum of SS is concerned, we only have to focus on what the first term of the scoring rule does. The second term is the good old log-likelihood so we know that part works.

After some math, one can show that scheduled sampling with a fixed $\epsilon$ minimises the following divergence between the true $P$ and the model $Q$:

$$D_{SS}[P\|Q] = KL[P_{x_1}\|Q_{x_1}] + (1-\epsilon) \mathbb{E}_{z\sim Q_{x_1}} KL[P_{x_2}\|Q_{x_2\vert x_1=z}] + \epsilon KL[P_{x_2\vert x_1}\|Q_{x_2\vert x_1}]$$

Now, if $\epsilon=1$, we recover the Kullback-Leibler divergence between the joint $P_{x_1,x_2}$ and $Q_{x_1,x_2}$, which is what we expect as it corresponds to maximum likelihood estimation. However, as $\epsilon$ is annealed to $0$, the objective function is somewhat strange, whereby the conditional distribution $Q_{x_2\vert x_1}$ is pushed to model the marginal distribution $P_{x_2}$, instead of $P_{x_2\vert x_1}$ as one would expect. One can therefore see that the factorised $Q^{*} = P_{x_1}P_{x_2}$ minimises this objective function.

#### what this means for text modeling

Extrapolating from the two variable case to longer sequences, one can see that the scheduled sampling objective would fail if minimised properly until convergence. Consider the case when the $\epsilon\approx 0$ stage is reached in the annealing schedule. Now consider what the RNN has to do to predict the $n$th character in a string during training. It is fed a random prefix string that was generated by itself but never seen any real data. Then the RNN has to give a probabilistic forecast of what the $n$th character in the training sentence is, having seen none of the previous characters in the sentence.

The optimal model that minimises this objective would completely ignore all the characters in the sentence so far, but keep a simple linear counter that indexes where it is within the sentence. Then it would emit a character from an index-specific marginal distribution of characters. This is the equivalent of the factorised trivial solution above.

Yes, such a model would be better at "recovering from its own mistakes", because at every character it would start independently from what it has generated so far. But this is at the cost of paying no attention whatsoever as to what the prefix of the sentence was. I believe the reason why this trivial behaviour was not observed in the paper is that the authors did not run the optimisation until convergence, and did not implement the full gradient of the objective function, as they discuss in the paper.

#### Constructive part of criticism

#### What to do instead of SS?

So the observed problem was that RNNs trained via maximum likelihood are unable to recover from their own mistakes early on in a sentence, when they are used to generate.

`The main reason for the observed problem is that the log-likelihood is a local scoring rule`

The local property of scoring rules means that at training time we only ever evaluate the model $Q$ on actually observed datapoints. So if the RNN is faced with a prefix subsequence that was not in the dataset, God knows what it's going to complete that sentence with.

The proper (shall I say strictly proper) way to fix this issue is to use 

### Evaluating Generative Models

A key topic I'm very interested in is the choices of objective functions used in unsupervised learning and generative models. The key organising principle should be this: the objective function we use for training a probabilistic model should match the way we ultimately want to use the model. Yet, in unsupervised learning this is often overlooked and I think we lack clarity around what the models are used for and how they should be trained and evaluated. This paper tries to clarify this a bit in the context of generative models. I also want to mention that another ICLR submission this year also deals with this fundamental question: I highly recommend taking a look.

Here, I'm going to consider a narrow definition of generative models: models we actually want to use to generate samples from which are then shown to a human user/observer. This includes use-cases such as image captioning, texture generation, machine translation, speech synthesis and dialogue systems, but excludes things like unsupervised pre-training for supervised learning, semisupervised learning, data compression, denoising and many others. Very often people don't make this distinction clear when talking about generative models which is one of the reasons why there is still no clarity about what different objective functions do.

I argue that when the goal is to train a model that can generate natural-looking samples, maximum likelihood is not a desirable training objective. Maximum likelihood is consistent so it can learn any distribution if it is given infinite data and a perfect model class. However, under model misspecification and finite data (that is, in pretty much every practically interesting scenario), it has a tendency to produce models that overgeneralise.

#### KL divergence as a perceptual loss

Generative modelling is about finding a probabilistic model $Q$ that in some sense approximates the natural distribution of data $P$. When researchers (or users of their product) evaluate generative models for perceptual quality, they draw samples from it, then - for lack of a better word - eyeball the samples. In visual information processing this is often referred to as no-reference perceptual quality assessment \citep[see e.,g.\ ][]{wang2002noreference}. In the paper, I propose that the KL divergence $KL[Q\| P]$ can be used as an idealised objective function to describe this scenario. This related to maximum likelihood which minimises $KL[P\|Q]$, but different in fundamental ways which I will explain later.

Here is why I think $KL[Q\|P]$ should be used: First, we can make the assumption that the perceived quality of each sample is related to the \emph{surprisal} $-\log Q_{human}(x)$ under the human observers' subjective prior of stimuli $Q_{human}(x)$. For those of you not familiar with computational cognitive science, this will seem ad-hoc, but it's a relatively common assumption to make when modelling reaction times in experiments for example. We further assume that the human observer maintains a very accurate model of natural stimuli, thus, $Q_{human}(x) \approx P(x)$. This is a fancy way of saying things like the observer being a native speaker therefore understanding all the nuances in language. These two assumptions suggest that in order to optimise our chances in this Turing test-like scenario, we need to minimise the following cross-entropy or perplexity term:

\begin{equation} - \mathbb{E}_{x\sim Q} \log P(x) \end{equation}

This perplexity is the exact opposite average negative log likelihood $- \mathbb{E}_{x\sim P} \log Q(x)$, with the role of $P$ and $Q$ changed. However, the perplexity alone would be maximised by a model $Q$ that deterministically picks the most likely stimulus. To enforce diversity one can simultaneously try to maximise the Shannon entropy of $Q$. This leaves us with the following KL divergence to optimise:

\begin{equation} KL[Q\| P] = - \mathbb{E}{x\sim Q} \log P(x) + \mathbb{E}{x\sim Q} \log Q(x) \end{equation}

So if we want to train models that produce nice samples, my recommendation is to try to use $KL[Q\|P]$ as an objective function or something that behaves like it. How does maximum likelihood compare?

#### Differences between maximum likelihood and $KL[Q\|P]$

Maximum likelihood is roughly the same as minimising $KL[P\|Q]$. The differences between minimising $KL[P\|Q]$ and $K[Q\|P]$ are well understood and it frequently comes up in the context of Bayesian approximate inference as well. Both divergences ensure consistency, minimising either converges to the true $P$ in the limit of infinite data and a perfect model class. However, they differ fundamentally in the way they deal with finite data and model misspecification (in almost every practical scenario):

$KL[P\|Q]$ tends to favour approximations $Q$ that overgeneralise $P$. If P is multimodal, the optimal $Q$ will tend to cover all the modes of $P$, even at the cost of introducing probability mass where $P$ has $0$ mass. Practically this means that the model will occasionally sample unplausible samples that don't look anything like samples from $P$.
$KL[Q\|P]$ tends to favour under-generalisation. The optimal $Q$ will typically describe the single largest mode of $P$ well, at the cost of ignoring other modes if they are hard to model without covering low-probability areas as well. Practically this means that $KL[Q\|P]$ will try to avoid introducing unplausible samples, sometimes at the cost of missing the majority of plausible samples under $P$.
In other words: $KL[P\|Q]$ is liberal, $KL[Q\|P]$ is conservative. In yet other words: $KL[P\|Q]$ is an optimist, $KL[Q\|P]$ is a pessimist.

The problem of course is that $KL[Q\|P]$ is super hard to optimise beased on a finite sample from $P$. Even harder than maximum likelihood. Not only that, the KL divergence is also not very well behaved, and is not well-defined unless $P$ is positive everywhere where $Q$ is positive. So there is little hope we can turn $KL[Q\|P]$ into a practical training algorithm.

#### Generalised Adversarial Training

Generative Adversarial Networks(GANs) train a generative model jointly with an adversarial discriminative model that tries to differentiate between artificial and real data. The idea is, a generative model is good if it can fool the best discriminative model into thinking the generated samples are real. GANs have produced some of the nicest looking samples you'll find on the Internet and got people very excited about generative models again: human faces, album covers, etc.

How do they come into this picture? It's because they can be understood as approximately minimising the Jensen-Shannon divergence:

\begin{equation} JSD[P\|Q] = JSD[P\|Q] = \frac{1}{2}KL\left[P\middle\|\frac{P+Q}{2}\right] + \frac{1}{2}KL\left[Q\middle\|\frac{P+Q}{2}\right]. 
\end{equation}

Looking at the equation above you can immediately see how it's related to this topic. JS divergence is a bit like a symmetrised version of KL divergence. It's not $KL[P\|Q]$, not $KL[Q\|P]$, but a bit of both. So one can expect that minimising JS divergence would exhibit a behaviour that is kind of halfway between the two extremes explained above. And that means that they would generate better samples than methods trained via maximum likelihood and similar objectives.

What's more, one can generalise JS divergence to a whole family of divergences, parametrised by a probability $0<\pi<1$ as follows:

\begin{equation} JS_{\pi}[P\|Q] = \pi \cdot KL[P\|\pi P+(1-\pi)Q] + (1-\pi)KL[Q\|\pi P+(1-\pi)Q]. 
\end{equation}

What I show in the paper is that by varrying $\pi$ between the two extremes, one can effectively interpolate between the behaviour of maximum likelihood ($\pi\rightarrow 0$) and minimising $KL[Q\|P]$ ($\pi\rightarrow 1$). See the paper for details. This interpolation between behaviours is explained in this main figure below:

![](http://www.inference.vc/content/images/2015/11/Screen-Shot-2015-11-16-at-16-19-10.png)

For any given value of $\pi$, we can optimise $JS_{\pi}$ approximately using an algorithm that is a slightly changed version of the original GAN algorithm. This is because the generalised JS divergence still has an elegant information theoretic interpretation. Consider a communications channel on which we can transmit a single data point of some kind. We toss a coin and with probability $\pi$, we send a sample from $P$, and with probability $1-\pi$ we send a sample from $Q$ instead. The receiver doesn't know the outcome of the coinflip, she only observes the sample. The $JS_{\pi}$ is the mutual information between the observed sample and the coinflip. It is also an upper bound on how well any algorithm can do in guessing the coinflip from the observed sample.

To implement an adversarial training algorithm for $JS_{\pi}$ one simply needs to change the ratio of samples the discriminative network sees from $Q$ vs $P$ (or apply appropriate weights during training). In the original method the discriminator network is faced with a balanced classification problem, i.e. $\pi=\frac{1}{2}$. It is hard to believe, but this irrelevant-looking modification changes the behaviour of the GAN algorithm dramatically, and can in theory allow the GAN algorithm to approximate both maximum likelihood or $KL[Q\|P]$.

This analysis explains why GANs have been so successful in generating very nice looking images, and relatively few weird-looking ones. It is also worth pointing out that the GAN method is still in its infantcy and has many issues and limitations. The main issue is that it is based on sampling from $Q$ which doesn't work well in high dimensions. Hopefully some of these limitations can be overcome and then we should have a pretty powerful framework for training good generative models.

#### Explainability-Accuracy trade-off

Many practical applications of machine learning systems call for the ability to explain why certain predictions are made. Consider a fraud detection system: it is not very useful for a user to see a list of possible fraud attempts without any explanation why the system thought the attempt was fraud. You want to say something like 'the system thinks it's fraud because the credit card was used to make several transactions that are smaller than usual'. But such explanations are not always compatible with our machine learning model. Or are they?

When choosing a machine learning model we usually think in terms of two choices:

- accurate but black-box: The best classification accuracy is typically achieved by black-box models such as Gaussian processes, neural networks or random forests, or complicated ensembles of all of these. Just look at the kaggle leaderboards. These are called black-box and are often criticised because their inner workings are really hard to understand. They don't, in general, provide a clear explanation of the reasons they made a certain prediction, they just spit out a probability.

- white-box but weak: On the other end of the spectrum, models whose predictions are easy to understand and communicate are usually very impoverished in their predictive capacity (linear regression, a single decision tree) or are inflexible and computationally cumbersome (explicit graphical models).

So which ones should we use: accurate black-box models, or less accurate but easy-to-explain white-box models?

The paper basically tells us that this is a false tradeoff. To summarise my take-home from this poster in one sentence:

`Explainability is not a property of the model`

Ryan presents a nice way to separate concerns of predictive power and explanation generation. He does this by introducing a formal framework in which simple, human-readable explanations can be generated for any black-box classifier, without assuming anything about the internal workings of the classifier.

If you think about it, it makes sense. If you watch someone playing chess, you can probably post-rationalise and give a reason why the person might think it's a good move. But you probably don't have an idea about the algorithm the person was executing in his brain.

Now we have a way to explain why decisions were made by complex systems, even if that explanation is not an exact explanation of what the classifier algorithm actually did. This is super-important in applications such as face recognitions where the only models that seem to work today are large black-box models. As (buzzword alert) AI-assisted decision making is becoming commonplace, the ability to generate simple explanations for black-box systems is going to be super important, and I think Ryan has made some very good observations in this paper.

I recommend everyone to take a look, I'm definitely going to see the world a bit differently after reading this.

#### Summary of this post: 

* an overview the motivation behind adversarial autoencoders and how they work * a discussion on whether the adversarial training is necessary in the first place. tl;dr: I think it's an overkill and I propose a simpler method along the lines of kernel moment matching.

#### Adversarial Autoencoders

Again, I recommend everyone interested to read the actual paper, but I'll attempt to give a high level overview the main ideas in the paper. I think the main figure from the paper does a pretty good job explaining how Adversarial Autoencoders are trained:

![](http://www.inference.vc/content/images/2016/01/Screen-Shot-2016-01-08-at-14-48-25.png)

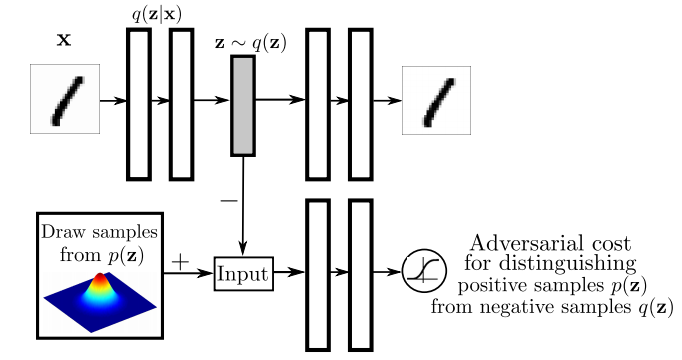
The top part of this image is a probabilistic autoencoder. Given the input $\mathbf{x}$, some latent code $\mathbf{z}$ is generated by sampling from an encoding distribution $q(\mathbf{z}\vert\mathbf{x})$. This distribution is typically modeled as the output a deep neural network. In normal autoencoders this encoder would be deterministic, now we allow it to be probabilistic.

A decoder network is then trained to decode $\mathbf{z}$ and reconstruct the original input $\mathbf{x}$. Of course, reconstruction will not be perfect, but we train the networks to minimise reconstruction error, this is typically just mean squared error.

The reconstruction cost ensures that the encoding process retains information about the input image, but it doesn't enforce anything else about what these latent representations $\mathbf{z}$ should do. In general, their distribution is described as the aggregate posterior $q(\mathbf{z})=\mathbb{E}_\mathbf{x} q(\mathbf{z}\vert\mathbf{x})$. Often, we would like this distribution to match a certain prior $p(\mathbf{z})$. For example. we may want $\mathbf{z}$ to have independent components and Gaussian distributed (nonlinear ICA,PCA). Or we may want to force the latent representations to correspond to discrete class labels, or binary factors. Or we may simply want to ensure there are 'no gaps' in the latent space, and any random $\mathbf{z}$ would lead to a viable sample when squashed through the decoder network.

So there are multiple reasons why one might want to control the aggregate posterior $q(\mathbf{z})$ to match a predefined prior $p(\mathbf{z})$. The authors achieve this by introducing an additional term in the autoencoder loss function, one that measures the divergence between $q$ and $p$. The authors chose to do this via adversarial training: they train a discriminator network that constantly learns to discriminate between real code vectors $\mathbb{z}$ produced by encoding real data, and random code vectors sampled from $p$. If $q$ matches $p$ perfectly, the optimal discriminator network should have a large classification error.

#### Is this an overkill?

My main question about this paper was whether the adversarial cost is really needed here, because I think it's an overkill. Let me explain:

Adversarial training is powerful when all else fails to quantify divergence between complicated, potentially degenerate distributions in high dimensions, such as images or video. Our toolkit for dealing with images is limited, CNNs are the best tool we have, so it makes sense to incorporate them in training generative models for images. GANs - when applied directly to images - are a great idea.

However, here adversarial training is applied to an easier problem: to quantify the divergence between a simple, fixed prior (e.g. Gaussian) and an empirical distribution of latents. The latent space is usually lower-dimensional, distributions better behaved. Therefore, matching to $p(\mathbf{z})$ in latent space should be considerably easier than matching distributions over images.

Adversarial training makes no assumptions about the distributions compared, other than sampling from them. This comes very handy when both $p$ and $q$ are nasty such as in the generative adversarial network scenario: there, $p$ is the distribution of natural images, $q$ is a super complicated, degenerate distribution produced by squashing noise through a deep convnet. The price we pay for this flexibility is this: when $p$ or $q$ are actually easy to work with, adversarial training cannot exploit that, it still has to sample. (it would be interesting to see if expectations over $p(\mathbf{z})$ could be computed analytically). So even though in this work $p$ is as simple as a mixture of ten 2D Gaussians, we need to approximate everything by drawing samples.

#### Other things might work: kernel moment matching

Why can’t one use easier divergences? For example, I think moment matching based on kernel MMD would work brilliantly in this scenario. It would have the following advantages over the adversarial cost.

- closed form expressions: Depending on the choice of the prior $p(\mathbf{z})$ and kernel used in MMD, the expectations over $p$ may be available in closed form, without sampling. So for example if we use a squared exponential kernel and a mixture of Gaussians as $p$, the divergence from $p$ can be precomputed in closed form that is easy to evaluate.

- no nasty inner loop: Adversarial training requires the discriminator network to be reoptimised every time the generative model changes. So we end up with a gradient descent in the inner loop of a gradient descent, which is anything but nice to work with. This is why it takes so long to get it working, the whole thing is pretty unstable. In contrast, to evaluate MMD, the inner loop is not needed. In fact, MMD can also be thought of as the solution to a convex maximisation problem, but via the kernel trick the maximum has a closed form solution.

- the problem is well suited for MMD: because the distributions are smooth, and the space is nice and low-dimensional, MMD might work very well. Kernel-based methods struggle with complicated manifold-like structure of natural images, so I wouldn't expect MMD to be competitive with adversarial training if it is applied directly in the image space. Therefore, I actually prefer generative adversarial networks to generative moment matching networks. However, here we have an easier problem, simpler space, simpler distributions where MMD shines, and adversarial training is just not needed.

The core idea behind this paper is powerfully simple. The goal is to learn useful representations from unlabelled data, useful in the sense of helping supervised object classification. This paper does this by chopping up images into a set of little jigsaw puzzle, scrambling the pieces, and asking a deep neural network to learn to reassemble them in the correct constellation. A picture is worth a thousand words, so here is Figure 1 taken from the paper explaining this visually:

![](http://www.inference.vc/content/images/2016/04/Screen-Shot-2016-04-25-at-08-26-45-1.png)

#### Summary of this note:

- I note the similarities to denoising autoencoders, which motivate my question: "Can this method equivalently represent the data generating distribution?"
- I consider a toy example with just two jigsaw pieces, and consider using an objective like this to fit a generative model $Q$ to data
- I show how the jigsaw puzzle training procedure corresponds to minimising a difference of KL divergences
- Conclude that the algorithm ignores some aspects of the data generating distribution, and argue that in this case it can be a good thing

#### What does this learn do?

This idea seems to make a lot of sense. But to me, one interesting question is the following:

`What does a network trained to solve jigsaw puzzle learn about the data generating distribution?`

#### Motivating example: denoising autoencoders

At one level, this jigsaw puzzle approach bears similarities to denoising autoencoders (DAEs): both methods are self-supervised: they take an unlabelled data and generate a synthetic supervised learning task. You can also interpret solving jigsaw puzzles as a special case 'undoing corruption' thus fitting a more general definition of autoencoders (Bengio et al, 2014).

DAEs have been shown to be related to score matching (Vincent, 2000), and that they learn to represent gradients of the log-probability-density-function of the data generating distribution (Alain et al, 2012). In this sense, autoencoders equivalently represent a complete probability distribution up to normalisation. This concept is also exploited in Harri Valpola's work on ladder networks (Rasmus et al, 2015)

So I was curious if I can find a similar neat interpretation of what really is going on in this jigsaw puzzle thing. If you equivalently represent all aspects of a probability distribution this way? Are there aspects that this representation ignores? Would it correspond to a consistent denisty estimation/generative modelling method in any sense? Below is my attempt to figure this out.

#### A toy case with just two jigsaw pieces

To simplify things, let's just consider a simpler jigsaw puzzle problem with just two jigsaw positions instead of 9, and in such a way that there are no gaps between puzzle pieces, so image patches (now on referred to as data $x$) can be partitioned exactly into pieces.

Let's assume our datapoints $x^{(n)}$ are drawn i.i.d. from an unknown distribution $P$, and that $x$ can be partitioned into two chunks $x_1$ and $x_2$ of equivalent dimensionality, such that $x=(x_1,x_2)$ by definition. Let's also define the permuted/scrambled version of a datapoint $x$ as $\hat{x}:=(x_2,x_1)$.

The jigsaw puzzle problem can be formulated in the following way: we draw a datapoint $x$ from $P$. We also independently draw a binary 'label' $y$ from a Bernoulli($\frac{1}{2}$) distribution, i.e. toss a coin. If $y=1$ we set $z=x$ otherwise $z=\hat{x}$.

Our task is to build a predictior, $f$, which receives as input $z$ and infers the value of $y$ (outputs the probability that its value is $1$). In other words, $f$ tries to guess the correct ordering of the chunks that make up the randomly scrambled datapoint $z$, thereby solving the jigsaw puzzle. The accuracy of the predictor is evaluated using the log-loss, a.k.a. binary cross-entropy, as it is common in binary classification problems:

$$ \mathcal{L}(f) = - \frac{1}{2} \mathbb{E}_{x\sim P} \left[\log f(x) + \log (1 - f(\hat{x}))\right] $$

Let's consider the case when we express the predictor $f$ in terms of a generative model $Q$ of $x$. $Q$ is an approximation to $P$, and has some parameters $\theta$ which we can tweak. For a given $\theta$, the posterior predictive distribution of $y$ takes the following form:

$$ f(z,\theta) := Q(y=1\vert z;\theta) = \frac{Q(z;\theta)}{Q(z;\theta) + Q(\hat{z};\theta)}, 
$$

where $\hat{z}$ denotes the scrambled/permuted version of $z$. Notice that when $f$ is defined this way the following property holds:

$$ 1 - f(\hat{x};\theta) = f(x;\theta), 
$$

so we can simplify the expression for the log-loss to finally obtain:

\begin{align} \mathcal{L}(\theta) &= - \mathbb{E}_{x \sim P} \log Q(x;\theta) + \mathbb{E}_{x \sim P} \log [Q(x;\theta) + Q(\hat{x};\theta)]\\ &= \operatorname{KL}[P\|Q_{\theta}] - \operatorname{KL}\left[P\middle\|\frac{Q_{\theta}(x)+Q_{\theta}(\hat{x})}{2}\right] + \log(2) \end{align}

So we already see that using the jigsaw objective to train a generative model reduces to minimising the difference between two KL divergences. It's also possible to reformulate the loss as:

$$ \mathcal{L}(\theta) = \operatorname{KL}[P\|Q_{\theta}] - \operatorname{KL}\left[\frac{P(x) + P(\hat{x})}{2}\middle\|\frac{Q_{\theta}(x)+Q_{\theta}(\hat{x})}{2}\right] - \operatorname{KL}\left[P\middle\|\frac{P(x) + P(\hat{x})}{2}\right] + \log(2) $$

Let's look at what the different terms do:

- The first term is the usual KL divergence that would correspond to maximum likelihood. So it just tries to make $Q$ as close to $P$ as possible.
- The second term is a bit weird, particularly as comes into the formula with a negative sign. The KL divergence is $0$ if $Q$ and $P$ define the distribution over the set of jigsaw pieces ${x_1,x_2}$. Notice, I used set notation here, so the ordering does not matter. In a way this term tells the loss function: don't bother modelling what the jigsaw pieces are, only model how they fit together.
- The last terms are constant wrt. $\theta$ so we don't need to worry about them.

#### Not a proper scoring rule (and it's okay)

From the formula above it is clear that the jigsaw training objective wouldn't be a proper scoring rule, as it is not uniquely minimised by $Q=P$ in all cases. Here are two counterexamples where the objective fails to capture all aspects of $P$:

Consider the case when $P=\frac{P(x) + P(\hat{x})}{2}$, that is, when $P$ is completely insensitive to the ordering of jigsaw pieces. As long as $Q$ also has this property $Q = \frac{Q(x) + Q(\hat{x})}{2}$, all KL divergences are $0$ and the jigsaw objective is constant with respect $\theta$. Indeed, it is impossible in this case for any classifier to surpass chance level in the jigsaw problem.

Another simple example to consider is a two-dimensional binary $P$. Here, the jigsaw objective only cares about the value of $Q(0,1)$ relative to $Q(1,0)$, but completely insensitive to $Q(1,1)$ and $Q(0,0)$. In other words, we don't really care how often $0$s and $1$s appear, we just want to know which one is likelier to be on the left or the right side.

This is all fine because we don't use this technique for generative modelling. We want to use it for representation learning, so it's okay to ignore some aspects of $P$.

#### Representation learning

I think this method seems like a really promising direction for unsupervised representation learning. In my mind representation learning needs either:

- strong prior assumptions about what variables/aspects of data are behaviourally relevant, or relevant to the tasks we want to solve with the representations.
- at least a little data in a semi-supervised setting to inform us about what is relevant and what is not.

Denoising autoencoders (with L2 reconstruction loss) and maximum likelihood training try to represent all aspects of the data generating distribution, down to pixel level. We can encode further priors in these models in various ways, either by constraining the network architecture or via probabilistic priors over latent variables.

The jigsaw method encodes prior assumptions into the training procedure: that the structure of the world (relative position of parts) is more important to get right than the low-level appearance of parts. This is probably a fair assumption.

- I give an overview of the paper which proposes an exponential schedule of dilated convolutional layers as a way to combine local and global knowledge
- I point out the connection between 2D dilated convolutions and Kronecker products
- cascades of exponentially dilated convolutions - as proposed in the paper - can be thought of as parametrising a large convolution kernel as a Kronecker product of small kernels
- the relationship to Kronecker factorisation only holds under particular assumptions, in this sense cascades of exponenetially diluted convolutions are a generalisation of the Kronecker layer (Zhou et al. 2015)
- I note that dilated convolutions are equivariant under image translation, a property that other multi-scale architectures often violate.

#### Background

The key application the dilated convolution authors have in mind is dense prediction: vision applications where the predicted object that has similar size and structure to the input image. For example, semantic segmentation with one label per pixel; image super-resolution, denoising, demosaicing, bottom-up saliency, keypoint detection, etc.

In many such applications one wants to integrate information from different spatial scales and balance two properties:

1. local, pixel-level accuracy, such as precise detection of edges, and
2. integrating knowledge of the wider, global context

To address this problem, people often use some kind of multi-scale convolutional neural networks, which often relies on spatial pooling. Instead the authors here propose using layers dilated convolutions, which allow us to address the multi-scale problem efficiently without increasing the number of parameters too much.

#### Dilated Convolutions

It's perhaps useful to first note why vanilla convolutions struggle to integrate global context. Consider a purely convolutional network composed of layers of $k\times k$ convolutions, without pooling. It is easy to see that size of the receptive field of each unit - the block of pixels which can influence its activation - is $l*(k-1)+k$, where $l$ is the layer index. So the effective receptive field of units can only grow linearly with layers. This is very limiting, especially for high-resolution input images.

Dilated convolutions to the rescue! The dilated convolution between signal $f$ and kernel $k$ and dilution factor $l$ is defined as:

$$ \left(k \ast_{l} f\right)_t = \sum_{\tau=-\infty}^{\infty} k_\tau \cdot f_{t - l\tau} $$

Note that I'm using slightly different notation than the authors. The above formula differs from vanilla convolution in last subscript $f_{t - l\tau}$. For plain old convolution this would be $f_{t - \tau}$. In the dilated convolution, the kernel only touches the signal at every $l^{th}$ entry. This formula applies to a 1D signal, but it can be straightforwardly extended to 2D convolutions.

The authors then build a network out of multiple layers of diluted convolutions, where the dilation factor $l$ increases exponentially at each layer. When you do that, even though the number of parameters grows only linearly with layers, the effective receptive field of units grows exponentially with layer depth. This is illustrated in the figure below:

![](http://www.inference.vc/content/images/2016/05/Screen-Shot-2016-05-12-at-09-47-12.png)

What this figure doesn't really show is the parameter sharing and parameter dependencies across the receptive field (frankly, it's pretty hard to visualise exactly with more than 2 layers). The receptive field grows at a faster rate than the number of parameters, and it is obvious that this can only be achieved by introducing additional constraints on the parameters across the receptive field. The network won't be able to learn arbitrary receptive field behaviours, so one question is, how severe is that restriction?

#### Relationship to Kronecker Products

To me this whole dilated convolution paper cries Kronecker product, although this connection is never made in the paper itself. It's easy to see that a 2D dilated convolution with matrix/filter $K$ is the same as vanilla convolution with a diluted filter $\hat{K}_{l}$ which can be represented as the following Kronecker product:

$$ \hat{K}_l = K \otimes \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 
0 & 0 & \ddots & & 0 \\ 
0 & \ddots & \ddots & \ddots & \\ 
0 & & \ddots & \ddots & 0 \\ 
0 & 0 & 0 & 0 & 0 
\end{bmatrix} $$

Using this, and properties of convolutions and Kronecker products (I suggest beginners to make extensive use of the matrix cookbook) we can even understand something about exponentially iterated dilated convolutions.

Let's assume we apply several layers of dilated convolutions, without nonlinearity, as in Equation 3 of the paper. For simplicity, I assume that that all convolution kernels $K_l, L=1\ldots L$ are $a\times a$ in size, the dilation factor at layer $l$ is $a^{l}$, and we only have a single channel throughout ($C=1$). In this case we can show that:

$$ F_{L+1} = K_L \ast_{a^L} \left( K_{L-1} \ast_{a^{(L-1)}} \left( \cdots K_1 \ast_{a} \left( K_0 \ast F_0 \right) \cdots \right) \right) = \left( K_L \otimes K_{L-1} \otimes \cdots \otimes K_{0} \right) \ast F_0 
$$

The left-hand side of this equation is the same construction as in Equation 3 in the paper, but expanded. The right hand side is a single vanilla convolution, but with a convolution kernel that is constructed as the Kronecker product of all the $a\times a$ kernels $K_l$.

It turns out Kronecker-factored parametrisations of convolution tensors are already used in CNNs, a quick googling revealed this paper:

Shuchang Zhou, Jia-Nan Wu, Yuxin Wu, Xinyu Zhou (2015) Exploiting Local Structures with the Kronecker Layer in Convolutional Networks
What can Kronecker-factored filters represent?

Let's look at what kind of kernels can we represent with Kronecker products, and hence what behaviour should we expect from dilated convolutions. Here are a few examples of $27\times 27$ kernels that result from taking the Kronecker product of three random $3\times 3$ kernels:

![](http://www.inference.vc/content/images/2016/05/VzORx0FEfAAAAAElFTkSuQmCC.png)

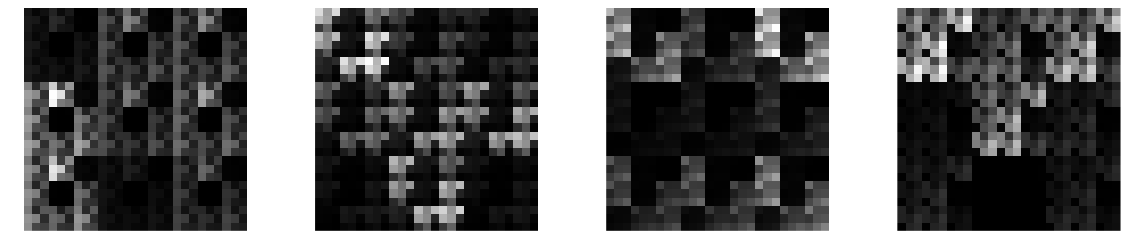
These look somehow natural, at least to me. They look like pretty plausible texture patches taken from some pixellated video game. You will notice the repeated patterns and the hierarchical structure. Indeed, we can draw cool self-similar fractal-like filters if we keep taking the Kronecker product of the same kernel with itself, some examples of such random fractals:

![](http://www.inference.vc/content/images/2016/05/YSJIkSZIkLYw3bCRJkiRJkhbGGzaSJEmSJEkL8zeSmRmMrhHPQgAAAABJRU5ErkJggg--.png)

I would say these kernels are not entirely unreasonable for a ConvNet, and if you allow for multiple channels ($C>1$) they can represent pretty nice structured patterns and shapes with reasonable number of parameters.

Compare these filters to another common technique for reducing parameters of convolution tensors: low-rank decompositions (see e.g. Lebedev et al, 2014). Spatially, a low-rank approximation to a square 2D convolution filter can be understood as subsequently applying two smaller rectangular filters: one with a limited horizontal extent and one with limited vertical extent. Here are a few random samples of $27\times 27$ filters with a rank of 1. These can be represented using the same number of parameters (27) as the Kronecker samples above.



To me, these don't look so natural. Notice also that for low-rank representations the number of parameters has to scale linearly with the spatial extent of the filter, whereas this scaling can be logarithmic if we use a Kronecker parametrisation. This is the real deal when using Kronecker products or dilated convolutions.

Here is another cool illustration of the naturalness of the Kronecker approximation, taken out of the Kronecker layer paper:

![](http://www.inference.vc/content/images/2016/05/Screen-Shot-2016-05-12-at-14-58-33.png)

So in general, parametrising convolution kernels as Kronecker-products seems like a pretty good idea. The dilated convolutions paper presents a more flexible approach than just Kronecker-factors. Firstly, you can add nonlinearities after each layer of dilated convolution, which would now be different from Kronecker products. Secondly, the Kronecker analogy only holds if the dilation factor and the kernel size are the same. In the paper the authors used a kernel size of $3$ and dilation factor of $2$.

#### Final note on translational equivariance

One desirable property of convolutions is that they are translationally equivariant: if you shift the input image by any amount, the output remains the same, shifted by the same amount. This is a very useful inductive bias/prior assumtion to use in a dense prediction task.

One way to introduce multiscale thinking to ConvNets is to use architectures that look like the figure below: we first decrease the spatial extent of feature-maps via pooling, then grow them back again via unpooling/deconvolution. Additional shortcut connections ensure that pixel-level local accuracy can be retained. The example below is from the SegNet paper, but there are multiple other papers such as this one on recombinator networks.

![](http://www.inference.vc/content/images/2016/05/conv-deconv.png)

However, as soon as you include spatial pooling, the translational equivariance property of the whole network might break. For example the SegNet above is not translationally equivariant anymore: the network's predictions are sensitive to small, single-pixel shifts to the input image, which is undesirable. Thankfully, layers of dilated convolutions are still translationally equivariant, which is a good thing.

#### Summary

This dilated convolutions idea is pretty cool, and I think these papers are just scratching the surface of this topic. The dilated convolution architecture generalises Kronecker-factored convolutional filters, it allows for very large receptive fields while only growing the number o

Summary of this post

 - How does this minibatch discrimination heuristic work and how does it change the behaviour of the GAN algorithm? Does it change the underlying objective function that is being minimized?
 - the answer is: for the original GAN algorithm that minimises Jensen-Shannon divergence it does change the behaviour in a non-trivial way. One side-effect is assigning a higher relative penalty for low-entropy generators.
 - when using the blended update rule from here, the algorithm minimises the reverse KL-divergence. In this case, using minibatch discrimination leaves the underlying objective unchanged: the algorithm can still be shown to miminise KL divergence.
 - even if the underlying objectives remain the same, using minibatch discrimination may be a very good idea practically. It may stabilise the algorithm by, for example, providing a lower variance estimator to log-probability-ratios.

[Here is the ipython/jupyter notebook](https://gist.github.com/fhuszar/a91c7d0672036335c1783d02c3a3dfe5) I used to draw the plots and test some of the things in this post in practice.

### What is minibatch discrimination?

In the vanilla Generative Adversarial Networks (GAN) algorithm, a discriminator is trained to tell apart generated synthetic examples from real data. One way GAN training can fail is to massively undershoot the entropy of the data-generating distribution, and concentrate all it's parameters on generating just a single or few examples.

To remedy this, the authors play with the idea of discriminating between whole minibatches of samples, rather than between individual samples. If the generator has low entropy, much lower than real data, it may be easier to detect this with a discriminator that sees multiple samples.

Here, I'm going to look at this technique in general: modifying an unsupervised learning algorithm by replacing individual samples with i.i.d. minibatches of samples. Note, that this is not exactly what the authors end up doing in the paper referenced above, but it's an interesting trick to think about.

#### How does the minibatch heuristic effect divergences?

The reason I'm so keen on studying GANs is the connection to principled information theoretic divergence criteria. Under some assumptions, it can be shown that GANs minimise the Jensen-Shannon (JS) divergence, or with a slight modification the reverse-KL divergence. In fact, a recent paper showed that you can use GAN-like algorithms to minimise any $f$-divergence.

So my immediate question looking at the minibatch discrimination idea was: how does this heuristic change the divergences that GANs minimise.

#### KL divergence

Let's assume we have any algorithm (GAN or anything else) that minimises KL divergence $\operatorname{KL}[P\|Q]$ between two distributions $P$ and $Q$. Let's now modify this algorithm so that instead of looking at distributions $P$ and $Q$ of a single sample $x$, it looks at distributions $P^{(N)}$ and $Q^{(N)}$ of whole a minibatch $(x_1,\ldots,x_N)$. I use $P^{(N)}$ to denote the following distribution:

$$ P^{(N)}(x_1,\ldots,x_N) = \prod_{n=1}^N P(x_n) 
$$

The resulting algorithm will therefore minimise the following divergence:

$$ d[P\|Q] = \operatorname{KL}[P^{(N)}\|Q^{(N)}] 
$$

It is relatively easy to show why this divergence $d$ behaves exactly like the KL divergence between $P$ and $Q$. Here's the maths for minibatch size of $N=2$:

\begin{align} d[P\|Q] &= \operatorname{KL}[P^{(2)}\|Q^{(2)}] \\ 
&= \mathbb{E}_{x_1\sim P,x_2\sim P}\log\frac{P(x_1)P(x_2)}{Q(x_1)Q(x_2)} \\ &= \mathbb{E}_{x_1\sim P,x_2\sim P}\log\frac{P(x_1)}{Q(x_1)} + \mathbb{E}_{x_1\sim P,x_2\sim P}\log\frac{P(x_2)}{Q(x_2)} \\ &= \mathbb{E}_{x_1\sim P}\log\frac{P(x_1)}{Q(x_1)} + \mathbb{E}_{x_2\sim P}\log\frac{P(x_2)}{Q(x_2)} \\ &= 2\operatorname{KL}[P\|Q] \end{align}

In full generality we can say that:

$$ \operatorname{KL}[P^{(N)}\|Q^{(N)}] = N \operatorname{KL}[P\|Q] $$

So changing the KL-divergence to minibatch KL-divergence does not change the objective of the training algorithm at all. Thus, if one uses minibatch discrimination with the blended training objective, one can rest assured that the algorithm still performs approximate gradient descent on the KL divergence. It may still work differently in practice, for example by reducing the variance of the estimators involved.

This property of the KL divergence is not surprising if one considers its compression/information theoretic definition: the extra bits needed to compress data drawn from $P$, using model $Q$. Compressing a minibatch of i.i.d. samples corresponds to compressing the samples independently. Their codelengths would add up linearly, hence KL-divergences add up linearly, too.

#### JS divergence

The same thing does not hold for the JS-divergence. Generally speaking, minibatch JS divergence behaves differently from ordinary JS-divergence. Instead of equality, for JS divergences the following inequality holds:

$$ JS[P^{(N)}\|Q^{(N)}] \leq N \cdot JS[P\|Q] 
$$

In fact for fixed $P$ and $Q$, $JS[P^{(N)}\|Q^{(N)}]/N$ is monotonically non-increasing. This can be seen intuitively by considering the definition of JS divergence as the mutual information between the samples and the binary indicator $y$ of whether the samples were drawn from $Q$ or $P$. Using this we have that:

\begin{align} \operatorname{JS}[P^{(2)}\|Q^{(2)}] &= \mathbb{I}[y ; x_1, x_2] \\ &= \mathbb{I}[y ; x_1] + \mathbb{I}[y ; x_2 \vert x_1] \\ &\leq \mathbb{I}[y ; x_1] + \mathbb{I}[y ; x_2] \\ &= 2 \operatorname{JS}[P\|Q] \end{align}

Below I plotted the minibatch-JS-divergence $JS[P^{(N)}\|Q^{(N)}]$ for various minibatch-sizes $N=1,2,3,8$, between univariate Bernoulli distributions with parameters $p$ and $q$. For the plots below, $p$ is kept fixed at $p=0.2$, and the parameter $q$ is varied between $0$ and $1$.

![](http://www.inference.vc/content/images/2016/06/fr9ra2qB2t9stl8sVnqIAAH1GqAAAhM3YsWOVkpKiTz75RD6fL9D-0UcfhbEqAEBfRYe7AABA5DIMQ-vXr9eLL76op556So8--qjOnDmjsrIyGYYR7vIAAL3ESAUAIKxmzpyp9957T52dndqyZYuOHTum4uJi7v4EAIMIIxUAgLCbPn26pk-fHtj2er1hrAYA0FeMVAAAAAAICaECAAAAQEgIFQCAm5JhGFysDQCDhOHnSjgAAAAAIWCkA.png)

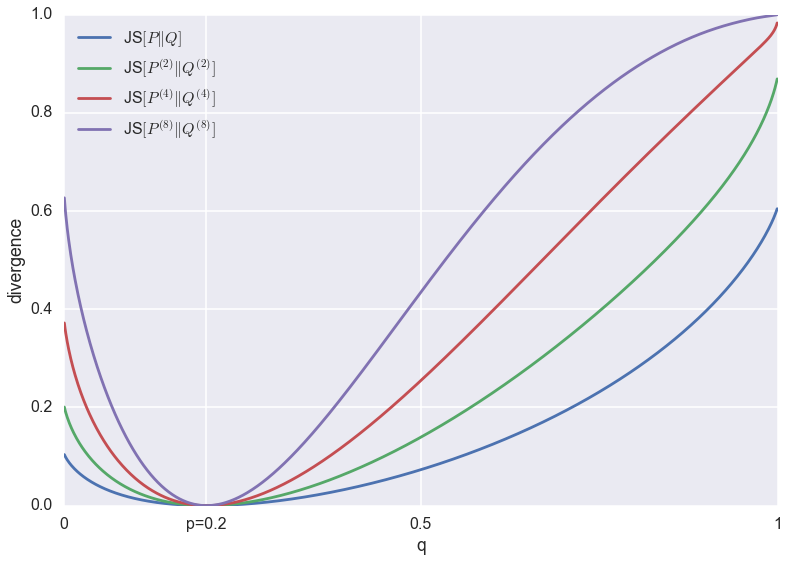
You can see that all divergences have a unique global minimum around $p=q=0.2$. However, their behaviour at the tails changes as the minibatch-size increases. This change in behaviour is due to saturation: JS divergence is upper bounded by $1$, which corresponds to 1 bit of information. If I continued increasing the minibatch-size (which would blow up the memory footprint of my super-naive script), eventually the divergence would reach $1$ almost everywhere except for a dip down to $0$ around $p=q=0.2$.

Below are the same divergences normalised to be roughly the same scale.

![](http://www.inference.vc/content/images/2016/06/Rle8idcTS3gAAAABJRU5ErkJggg--.png)

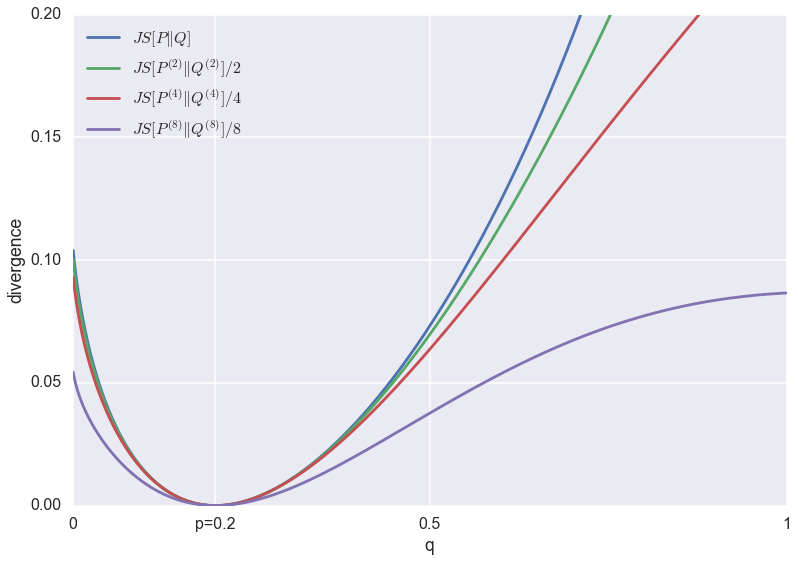
The problem of GANs that minibatch discrimination was meant to fix is that it favours low-entropy solutions. In this plot, this would correspond to the $q<0.1$ regime. You can argue that as the batch-size increases, the relative penalty for low-entropy approximations $q<0.1$ do indeed decrease when compared to completely wrong solutions $q>0.5$. However, the effect is pretty subtle.

Bonus track: adversarial preference loss

In this context, I also revisited the adversarial preference loss. Here, the discriminator receives two inputs $x_1$ and $x_2$ (one synthetic, one real) and it has to decide which one was real.

This algorithm, too, can be related to the minibatch discrimination approach, as it minimises the following divergence:

$$ d(P,Q) = d(P\times Q\|Q\times P), 
$$

where $P\times Q(x_1,x_2) = P(x_1)Q(x_2)$. Again, if $d$ is the $KL$ divergence, the training objective boils down to the same thing as the original GAN. However, if $d$ is the JS divergence, we will end up minimising something weird, $\operatorname{JS}[Q\times P\| P\times Q]$

"Aapo did it again!" - I exclaimed while reading this paper yesterday on the train back home (or at least I thought I was going home until I realised I was sitting on the wrong train the whole time. This gave me a couple more hours to think while traveling on a variety of long-distance buses...)

Aapo Hyvärinen is one of my heroes - he did tons of cool work, probably most famous for pseudo-likelihood, score matching and ICA. His recent paper, brought to my attention by my brand new colleague Hugo Larochelle, is similarly excellent:

### Summary

Time-contrastive learning (TCL) trains a classifier that looks at a datapoint and guesses what part of the time series it came from.
it exploits nonstationarity of time series to help representation learning
an elegant connection to generative models (nonlinear ICA) is shown, although the assumptions of the model are pretty limiting
TCL is the temporal analogue of representation learning with jigsaw puzzles
similarly to GANs, logistic regression is deployed as a proxy to learn log-likelihood ratios directly from data
Time-contrastive learning

Time-contrastive learning (TCL) is a technique for learning to extract nonlinear representations from time series data. First, the time series is sliced up into a number of non-overlapping chunks, indexed by ττ. Then, a multivariate logistic regression classifier is trained in a supervised manner to look at a sample taken from the series at an unknown time and predict ττ, the index of the chunk it came from. For this classifier, a neural network is used.

The classifier itself is only a proxy to solving the representation learning problem. It turns out, if you chop off the final linear + softmax layer, the activations in the last hidden layer will learn to represent something fundamental, the log-odds-ratios in a probabilistic generative model (see paper for details). If one runs linear ICA over these hidden layer activations, the resulting network will learn to perform inference in a nonlinear ICA latent variable model.

Moreover, if certain conditions about nonstationarity and the generative model are met, one can prove that the latent variable model is identifiable. This means that if the data was indeed drawn from the nonlinear ICA generative model, the resulting inference network - composed by the chopping off the top of the classifier and replacing it with a linear ICA layer - can infer the true hidden variables exactly.

### How practical are the assumptions?

TCL relies on the nonstationarity of time series data: the statistics of data changes depending on which chunk or slice of the time series you are in, but it is also assumed that data are i.i.d. within each chunk. The proof also assumes that the chunk-conditional data distributions are slightly modulated versions of the same nonlinear ICA generative model, this is how the model ends up identifiable - because we can use the different temporal chunks as different perspectives on the latent variables.

I would say that these assumptions are not very practical, or at least on data such as natural video. Something along the lines of slow-feature analysis, with latent variables that exhibit more interesting behaviour over time would be desirable. Nevertheless, the model is complex enough to make a point, and I beleive TCL itself can be deployed more generally for representation learning.

### Temporal jigsaw

It's not hard to see that TCL is analogous to a temporal version of the jigsaw puzzle method I wrote about last month. In the jigsaw puzzle method, one breaks up a single image into non-overlapping chunks, shuffles them, and then trains a network to reassemble the pieces. Here, the chunking happens in the temporal domain instead.

There are other papers that use the same general idea: training classifiers that guess the correct temporal ordering of frames or subsequences in videos. To do well at their job, these classifiers can end up learning about objects, motion, perhaps even a notion of inertia, gravity or causality.

Ishan Misra et al. (2016) Unsupervised Learning using Sequential Verification for Action Recognition
Basura Fernando et al. (2015) Modeling Video Evolution For Action Recognition
In this context, the key contribution of Hyvarinen and Morioka's paper is to provide extra theoretical justification, and relating the idea to generative models. I'm sure one can use this framework to extend TCL to slightly more plausible generative models.

### Key takeaway

`Logistic regression learns likelihood ratios`

This is yet another example of using logistic regression as a proxy to estimating log-probability-ratios directly from data. The same thing happens in generative adversarial networks, where the discriminator learns to represent $\log P(x) - \log Q(x)$, where $P$ and $Q$ are the real and synthetic data distributions, respectively.

This insight provides new ways in which unsupervised or semi-supervised tasks can be reduced to supervised learning problems. 
As classification is now considered significantly easier than density estimation, direct probability ratio estimation may provide the easiest path forward for representation learning.