The authors present an iterative approach for optimizing policies with guaranteed monotonic improvement.
TRPO is similar to natural policy gradient methods and can be applied effectively in optimization of large nonlinear policies.

\cite{KakadeL02} gave monotonic improvement guarantees for mixture of policies $\pi_{new}(a|s)=(1-\alpha)\pi_{old}(a|s) + \alpha\pi'(a|s)$ where $\pi'=\mathrm{arg}\max_{\pi'}L_{\pi_{old}}(\pi')$ is the approximated expected return of a policy $\pi'$ in terms of the advantage over $\pi_{old}$, as $\eta(\pi_{new})\geq L_{\pi_{old}}(\pi_{new}) - \frac{2\epsilon\gamma}{(1-\gamma)^2}\alpha^2$ with $\eta$ the true expected return and $\epsilon$ the maximally expected advantage.

The authors extend this approach to be applicable for all stochastic policy classes by replacing $\alpha$ with a distance measure between two policies $\pi_{new}$ and $\pi_{old}$.
As distance measure they use the maximal Kullback–Leibler divergence $D_{KL}^{\max}(\pi_{new},\pi_{old})$ and show that $\eta(\pi_{new})\geq L_{\pi_{old}}(\pi_{new}) -CD_{KL}^{\max}(\pi_{new},\pi_{old})$, with $C= \frac{4\epsilon\gamma}{(1-\gamma)^2}$.

From this follows, that one is guaranteed to improve the true objective $\eta$ when performing the following maximaization $\mathrm{maximize}_\pi\left[L_{\pi_{old}}(\pi)-CD_{KL}^{\max}(\pi,\pi_{old})\right]$. In practice however $C$ would only allow for small steps. Thus constraining $\mathrm{maximize}_\pi L_{\pi_{old}}(\pi)$ subject to $D_{KL}^{\max}(\pi,\pi_{old}) \leq \delta$ allows for larger steps in a **Trust Region**

Due to the large number of constraints this problem is impractical to solve, which is why the authors replace the maximum KL divergence with approximated average KL.

TRPO then works as follows:
 1. Use a rollout procedure to collet a set of state-action-pairs wit Monte Carlo estimates of their $Q$-Values
 2. Average over the samples to construct the estimate objective $L_{\pi}$ as well as the constraint
 3. Approximately solve the constrained optimization problem to update the policy parameters.
 They use the conjugate gradient algorithm followed by a linesearch.

Their experiments support the claim that TRPO is able to effectively optimize large nonlinear policies.

  * Generative Moment Matching Networks (GMMN) are generative models that use maximum mean discrepancy (MMD) for their objective function.
  * MMD is a measure of how similar two datasets are (here: generated dataset and training set).
  * GMMNs are similar to GANs, but they replace the Discriminator with the MMD measure, making their optimization more stable.

### How
  * MMD calculates a similarity measure by comparing statistics of two datasets with each other.
  * MMD is calculated based on samples from the training set and the generated dataset.
  * A kernel function is applied to pairs of these samples (thus the statistics are acutally calculated in high-dimensional spaces). The authors use Gaussian kernels.
  * MMD can be approximated using a small number of samples.
  * MMD is differentiable and therefor can be used as a standard loss function.
  * They train two models:
    * GMMN: Noise vector input (as in GANs), several ReLU layers into one sigmoid layer. MMD as the loss function.
    * GMMN+AE: Same as GMMN, but the sigmoid output is not an image, but instead the code that gets fed into an autoencoder's (AE) decoder. The AE is trained separately on the dataset. MMD is backpropagated through the decoder and then the GMMN. I.e. the GMMN learns to produce codes that let the decoder generate good looking images.

![Formula](https://raw.githubusercontent.com/aleju/papers/master/neural-nets/images/Generative_Moment_Matching_Networks__formula.png?raw=true "Formula")

*MMD formula, where $x_i$ is a training set example and $y_i$ a generated example.*


![Architectures](https://raw.githubusercontent.com/aleju/papers/master/neural-nets/images/Generative_Moment_Matching_Networks__architectures.png?raw=true "Architectures")

*Architectures of GMMN (left) and GMMN+AE (right).*


### Results
  * They tested only on MNIST and TFD (i.e. datasets that are well suited for AEs...).
  * Their GMMN achieves similar log likelihoods compared to other models.
  * Their GMMN+AE achieves better log likelihoods than other models.
  * GMMN+AE produces good looking images.
  * GMMN+AE produces smooth interpolations between images.

![Interpolations](https://raw.githubusercontent.com/aleju/papers/master/neural-nets/images/Generative_Moment_Matching_Networks__interpolations.png?raw=true "Interpolations")

*Generated TFD images and interpolations between them.*


--------------------

### Rough chapter-wise notes

* (1) Introduction
  * Sampling in GMMNs is fast.
  * GMMNs are similar to GANs.
  * While the training objective in GANs is a minimax problem, in GMMNs it is a simple loss function.
  * GMMNs are based on maximum mean discrepancy. They use that (implemented via the kernel trick) as the loss function.
  * GMMNs try to generate data so that the moments in the generated data are as similar as possible to the moments in the training data.
  * They combine GMMNs with autoencoders. That is, they first train an autoencoder to generate images. Then they train a GMMN to produce sound code inputs to the decoder of the autoencoder.

* (2) Maximum Mean Discrepancy
  * Maximum mean discrepancy (MMD) is a frequentist estimator to tell whether two datasets X and Y come from the same probability distribution.
  * MMD estimates basic statistics values (i.e. mean and higher order statistics) of both datasets and compares them with each other.
  * MMD can be formulated so that examples from the datasets are only used for scalar products. Then the kernel trick can be applied.
  * It can be shown that minimizing MMD with gaussian kernels is equivalent to matching all moments between the probability distributions of the datasets.

* (4) Generative Moment Matching Networks
  * Data Space Networks
    * Just like GANs, GMMNs start with a noise vector that has N values sampled uniformly from [-1, 1].
    * The noise vector is then fed forward through several fully connected ReLU layers.
    * The MMD is differentiable and therefor can be used for backpropagation.
  * Auto-Encoder Code Sparse Networks
    * AEs can be used to reconstruct high-dimensional data, which is a simpler task than to learn to generate new data from scratch.
    * Advantages of using the AE code space:
      * Dimensionality can be explicitly chosen.
      * Disentangling factors of variation.
    * They suggest a combination of GMMN and AE. They first train an AE, then they train a GMMN to generate good codes for the AE's decoder (based on MMD loss).
    * For some reason they use greedy layer-wise pretraining with later fine-tuning for the AE, but don't explain why. (That training method is outdated?)
    * They add dropout to their AE's encoder to get a smoother code manifold.
  * Practical Considerations
    * MMD has a bandwidth parameter (as its based on RBFs). Instead of chosing a single fixed bandwidth, they instead use multiple kernels with different bandwidths (1, 5, 10, ...), apply them all and then sum the results.
    * Instead of $MMD^2$ loss they use $\sqrt{MMD^2}$, which does not go as fast to zero as raw MMD, thereby creating stronger gradients.
    * Per minibatch they generate a small number of samples und they pick a small number of samples from the training set. They then compute MMD for these samples. I.e. they don't run MMD over the whole training set as that would be computationally prohibitive.

* (5) Experiments
  * They trained on MNIST and TFD.
  * They used an GMMN with 4 ReLU layers and autoencoders with either 2/2 (encoder, decoder) hidden sigmoid layers (MNIST) or 3/3 (TFD).
  * They used dropout on the encoder layers.
  * They used layer-wise pretraining and finetuning for the AEs.
  * They tuned most of the hyperparameters using bayesian optimization.
  * They use minibatch sizes of 1000 and compute MMD based on those (i.e. based on 2000 points total).
  * Their GMMN+AE model achieves better log likelihood values than all competitors. The raw GMMN model performs roughly on par with the competitors.
  * Nearest neighbor evaluation indicates that it did not just memorize the training set.
  * The model learns smooth interpolations between digits (MNIST) and faces (TFD).

This paper presents a model that can dynamically split computation across coarse, low-capacity sub-networks and fine, high-capacity sub-networks. The coarse model processes the entire input data and is typically shallow while the fine model focuses on a few important regions of the input and is deeper. For images as input, this is a hard attention mechanism that can be trained with stochastic gradient descent and doesn't require a task-specific attention policy trained by reinforcement learning. Key ideas:

- A deep network h can be decomposed into bottom layers f and top layers g such that $h(x) = g(f(x))$. Further, f consists of two alternate sub-networks $f\_c$ and $f\_f$. $f\_c$ is a low-capacity sub-network while $f\_f$ is a high-capacity sub-network.

- g should be able to use representations from $f\_c$ and $f\_f$ dynamically. $f\_c$ processes the entire input while $f\_f$ only a few important regions of the input.

- The coarse model processes the entire input and the norm of the gradient of the entropy with respect to the coarse vector at each spatial region is computed which is a measure of saliency. The use of the entropy gradient as a saliency measure encourages selecting input regions that could affect the uncertainty in the model’s predictions the most.

- The top-k input regions with highest saliency values are processed by the fine model. The refined representation for input to the top layers consists of both coarse and fine vectors. During backpropagation, gradients are computed for the refined model, i.e. propagating gradients at each position into either the coarse or fine features, depending on which was used.

- To make sure $f\_c$ and $f\_f$ representations are interchangeable and input to the top layers has smooth transitions, an additional objective term minimizes the squared distance between coarse and fine representations and this additional term is used only to optimize the coarse layers, not the fine layers.

- Experiments on cluttered MNIST, SVHN and comparison with RAM, DRAW and study with various values of number of patches for fine processing.

## Strengths

- Neat, general way to split computation based on importance of input; a hard-attention mechanism that can be trained with SGD, unlike RAM.

- Entropy gradient as a measure of saliency is an interesting idea, and it doesn't need labels i.e. can be used at test time.

I spend the week at ICML, and this paper on generative models is one of my favourites so far:

To be clear: this post doesn't add much to the presentation of the paper, but I will attempt to summarise my understanding of it. Also, I want to make clear that this is not my work.

Unsupervised learning has been one of the most interesting areas of machine learning in the last decades, but it is in the spotlight again since the deep learning crowd started to care about it. Unsupervised learning is hard because evaluating the loss function people want to use (log likelihood) is intractable for most interesting models. Therefore people come up with

- alternative objective functions, such as adversarial training, maximum mean discrepancy, or pseudolikelihood, which can be evaluated for a large class of interesting models
- alternative optimisation methods or approximate inference methods such as contrastive divergence or variational Bayes
- models that have some nice properties. This paper is an example of the latter

#### The key idea behind the paper

What we typically try to do in representation learning is to map data to a latent representation. While the Data can have arbitrarily complex distribution along some complicated nonlinear manifold, we want the computed latent representations to have a nice distribution, like a multivariate Gaussian.

This paper takes this idea very explicitly using a stochastic mapping to turn data into a representation: a random diffusion process. If you take any data, and apply Brownian motion-like stochastic process to this, you will end up with a standard Gaussian distributed variable, due to the stationarity of the Brownian motion. Below image shows an example: 2D observations (left) have a complex data distribution along the Swiss roll manifold. If one applies Brownian motion to each datapoint, the complicated structure starts to diffuse, and eventually the data is scrambled to become white noise (right).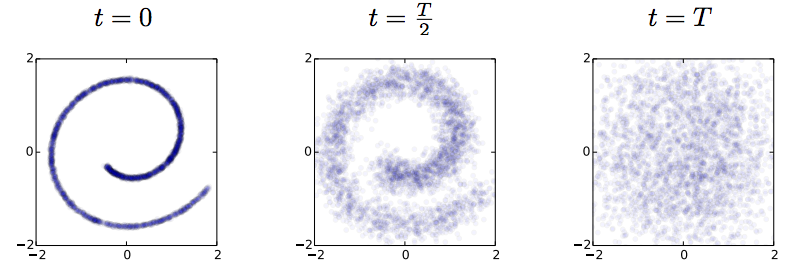

![](http://www.inference.vc/content/images/2015/07/Screen-Shot-2015-07-09-at-13-27-41.png)

Now the trick the authors used is to train a dynamical system to inverts this random walk, to be able to reconstruct the original data distribution from the random Gaussian noise. Amazingly, this works, and the traninig objective becomes very similar to variational autoencoders. Below is a figure showing what happens when we try to reconstruct data in the Swiss roll example: The top images from right to left: we start with a bunch of points drawn from random noise (top right). We apply the inverse nonlinear transformation to these points (top middle). Over time points will be pushed towards the original Swiss roll manifold (top left).

`The information about the data distribution is encoded in the approximate inverse dynamical system`

The bottom pictures show where this dynamical system tries to push points as time progresses.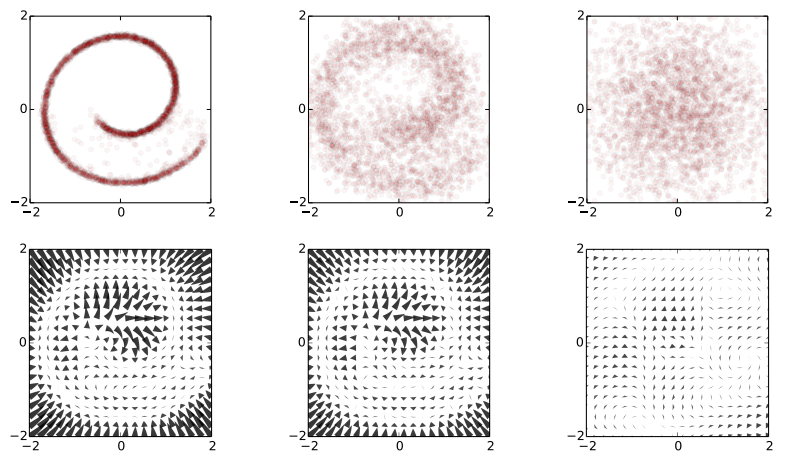

![](http://www.inference.vc/content/images/2015/07/Screen-Shot-2015-07-09-at-13-30-16.png)

This is super cool. Now we have a deep generative process that can turn random noise into something that looks like our datapoints. It can generate roughly natural-looking images like these:

![](http://www.inference.vc/content/images/2015/07/Screen-Shot-2015-07-09-at-13-33-38.png)

 #### Advantages

In this model a lot of things that are otherwise hard to do are easy to do:

1. generating/imagining data is straightforward
2. inference, i.e. calculating the latent representation from data, is simple
3. you can multiply the distribution with another distribution, making Bayesian calculations for stuff like denoising or superresolution possible.

#### Drawbacks and extensions

I think a drawback of the model is that if you run the diffusion process for too long (i.e. make the model deeper), the mutual information between datapoint and its representation is bound to decrease, due to the stationarity of Brownian motion. I guess this is going to be an important limitation to the depth of these models.

Also, the latent representations at each layer are assumed to be exactly if the same dimensionality and type as the data itsef. So if we are modeling 100x100 images, then all layers in the resulting network will have 100k nodes. I guess this can be overcome by combining variational autoencoders with this method. Also, you can imagine augmenting your space with extra 'pixels' that are only used for richer representations in the intermediate layers.

Anyway, this is super cool, go read the paper.

This is my second favourite paper from ICML last week, and I think the title really does not do it justice. It is a great idea about training rich, tractable autoregressive generative models of data, and doing so by using standard techniques from autoencoder training with dropout.

Caveat (again): this is not my work, and this blog post does not really add anything new to the paper, only my perspective on it.

#### Unsupervised learning primer (again)

Unsupervised learning is about modelling the probability distribution $p(\mathbf{x})$ of some data, from which we observe independent samples $\mathbf{x}_i$. Often, the vector $\mathbf{x}$ is high dimensional, such as in images, where different components of $\mathbf{x}$ encode pixel intensities.

Typically, a probability model is specified as $q(\mathbf{x};\theta) = \frac{f(\mathbf{x};\theta)}{Z_\theta}$, where $f(\mathbf{x};\theta)$ is some positive function parametrised by $\theta$. The denominator $Z_\theta$ is called the normalisation constant which makes sure that $q$ is a valid probability model: it has to sum up to one over all possible configurations of $\mathbf{x}$. The central problem in unsupervised learning is that for the most interesting models in high dimensional spaces, calculating $Z_\theta$ is intractable, so crucial quantities such as the model likelihood cannot be calculated and the model cannot be fitted. The community is therefore in search for

- interesting models that have tractable normalisation constants
- fancy methods to deal with intractable models (pseudo-likelihood, adversarial networks, contrastive divergence)

This paper is about the former.

#### Core ingredient: autoregressive models

This paper sidesteps the high dimensional normalisation problem by restricting the class of probability distributions to autoregressive models, which can be written as follows:

$$q(\mathbf{x};\theta) = \prod_{d=1}^{D} q(x_{d}\vert x_{1:d-1};\theta).$$

Here $x_d$ denotes the $d^{th}$ component of the input vector $\mathbf{x}$. In a model like this, we only need to compute the normalisation of each $q(x_{d}\vert x_{1:d-1};\theta)$ term, and we can be sure that the resulting model is a valid model over the whole vector $\mathbf{x}$. But as normalising these one-dimensional probability distributions is a lot easier, we have a whole range of interesting tractable distributions at our disposal.

#### Training multiple models simultaneously

Autoregressive models are used a lot in time series modelling and language modelling: hidden Markov models or recurrent neural networks are examples. There, autoregressive models are a very natural way to model data because the data comes ordered (in time).

What's weird about using autoregressive models in this context is that it is sensitive to ordering of dimensions, even though that ordering might not mean anything. If $\mathbf{x}$ encodes an image, you can think about multiple orders in which pixel values can be serialised: sweeping left-to-right, top-to-bottom, inside-out etc. For images, neither of these orderings is particularly natural, yet all of these different ordering specifies a different model above.

But it turns out, you don't have to choose one ordering, you can choose all of them at the same time. The neat trick in the masking autoencoder paper is to train multiple autoregressive models all at the same time, all of them sharing (a subset of) parameters $\theta$, but defined over different ordering of coordinates. This can be achieved by thinking of deep autoregressive models as a special cases of an autoencoder, only with a few edges missing.

![](http://www.inference.vc/content/images/2015/07/Screen-Shot-2015-07-13-at-10-48-54.png)

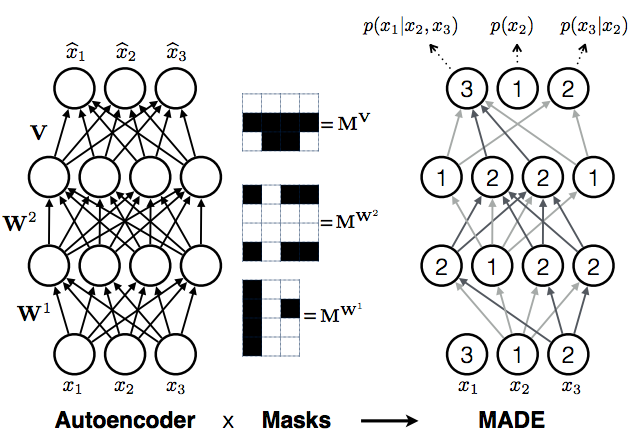
Consider a fixed ordering of input dimensions. Now take a fully connected autoencoder, which defines a probability distribution $q(\hat{\mathbf{x}}\vert\mathbf{x};\theta)$. You can write this as

$$q(\hat{\mathbf{x}}\vert\mathbf{x};\theta) = \prod_{d=1}^{D} q(\hat{x}_{d}\vert x_{1:D};\theta)$$

Note the similarity to the autoregressive equation above, the only difference being that each coordinate now depends on every other coordinate ($x_{1:D}$), rather than only coordinates that precede it in the ordering ($x_{1:d-1}$). To turn this equation into autoregressive equation above, we simply have to remove dependencies of each output coordinate $\hat{x}_{d}$ on any input coordinate $\hat{x}_{e}$, where $e>=d$. This can be done by removing edges along all paths from the input coordinate $\hat{x}_{e}$ to output coordinate $\hat{x}_{d}$. You can achieve this cutting of edges by multiplying the weight matrices $\mathbf{W}^{l}$of the autoencoder neural network elementwise by binary masking matrices $\mathbf{M}^{\mathbf{W}^{l}}$. Hence the name masked autoencoder.

The procedure above considered a fixed ordering of coordinates. You can repeat this process for any arbitrary ordering, for which you obtain different masking matrices but otherwise the same procedure. If you train this autoencoder network with randomly sampled masking matrices, you essentially train a family of autoregressive models, each sharing some parameters via the underlying autoencoder network.

Because masking is similar to the popular dropout training, implementing it is relatively straightforward and requires minimal change to existing autoencoder code. However, now you have a generative model - in fact, a large set of generative models - which has a lot of nice properties for you to enjoy.

The slight concern

Of course, this would be all too good to be true: a powerful deep generative model that is easy to evaluate and all. I think the problem with this is the following: If you train just one of these autoregressive models, that's tractable, exact and fine. But you really want to combine all (or many) of these becuause individually they are weak.

What is the interpretation of training with randomly drawn masking matrices? You can think of it as stochastic gradient descent on the following objective:

$$\mathbb{E}_{\mathbf{x}\sim p}\mathbb{E}_{\pi \sim U} \log q(\mathbf{x},\pi,\theta)$$

Here, I used $\pi$ to denote a permutation of the coordinates, and $\mathbb{E}_{\pi \sim U}$ to take an expectation over a uniform distribution over permutations. The distribution $q(\mathbf{x},\pi,\theta)$ is the autoregressive model defined by $\theta$ and the masking matrices corresponding to permutation $\pi$. $\mathbb{E}_{\mathbf{x}\sim p}$ denotes averaging over the empirical data distribution.

Combining as a mixture model

One way to combine autoregressive models is to take a mixture model. In the paper, the authors actually use an ensemble to make predictions, which is analogous to an equal mixture model where the mixture weights are uniform and fixed. The likelihood for this model would be the following:

$$\mathbb{E}_{\mathbf{x}\sim p} \log \mathbb{E}_{\pi \sim U} q(\mathbf{x},\pi,\theta)$$

Notice that the averaging over permutations now takes place inside the logarithm. By Jensen's inequality, we can say that randomly sampling masking matrices during training amounts to optimising a stochastically estimated lower bound to the likelihood of an equal mixture. This raises the question whether actually learning the weights in such a model would be hard using something like an EM algorithm with a sparsity-enforcing regulariser/prior over mixture weights.

Combining as a product of experts model

Combining these autoregressive models as a mixture is not ideal. In mixture modeling the sharpness of the mixture distribution is bounded by the sharpness of component distributions. Your combined prediction can never be more confident than the your most confident model. In this case, I expect the AR models to be pretty poor models individually, and therefore not to be very sharp, particularly along the first few coordinates in the corresponding ordering.

A better way to combine probabilistic models is via product of experts. You can actually interpret training by random masking matrices as a form of product of experts, but with the global normalisation ignored. I'm not sure if it would be possible/tractable to do anything better than this.

TLDR; The authors use an attention mechanism in image caption generation, allowing the decoder RNN focus on specific parts of the image. In order find the correspondence between words and image patches, the RNN uses a lower convolutional layer as its input (before pooling). The authors propose both a "hard" attention (trained using sampling methods) and "soft" attention (trained end-to-end) mechanism, and show qualitatively that the decoder focuses on sensible regions while generating text, adding an additional layer of interpretability to the model. The attention-based models achieve state-of-the art on Flickr8k, Flickr30 and MS Coco.

#### Key Points

- To find image correspondence use lower convolutional layers to attend to.
- Two attention mechanisms: Soft and hard. Depending on evaluation metric (BLEU vs. METERO) one or the other performs better.
- Largest data set (MS COCO) takes 3 days to train on Titan Black GPU. Oxford VGG.
- Soft attention is same as for seq2seq models.
- Attention weights are visualized by upsampling and applying a Gaussian

#### Notes/Questions

- Would've liked to see an explanation of when/how soft vs. hard attention does better.
- What is the computational overhead of using the attention mechanism? Is it significant?

This paper proposes a layers wise adaptive depth quantization of DCNs, giving an better tradeoff of error rate/ memory requirement than the fixed bit width across layers.

The authors describe an optimization problem for determining the bit-width for different layers of DCNs for reducing model size and required computation.

This paper builds further upon the line of research that tries to represent neural network weights and outputs with lower bit-depths. This way, NN weights will take less memory/space and can speed up implementations of NNs (on GPUs or more specialized hardware).

This is another "learning the learning rate" paper, which predates (and might have inspired) the "Speed learning on the fly" paper I recently wrote notes about (see \cite{journals/corr/MasseO15}). In this paper, they consider the off-line training scenario, and propose to do gradient descent on the learning rate by unrolling the *complete* training procedure and treating it all as a function to optimize, with respect to the learning rate. This way, they can optimize directly the validation set loss.

The paper in fact goes much further and can tune many other hyper-parameters of the gradient descent procedure: momentum, weight initialization distribution parameters, regularization and input preprocessing.

#### My two cents

This is one of my favorite papers of this year. While the method of unrolling several steps of gradient descent (100 iterations in the paper) makes it somewhat impractical for large networks (which is probably why they considered 3-layer networks with only 50 hidden units per layer), it provides an incredibly interesting window on what are good hyper-parameter choices for neural networks. Note that, to substantially reduce the memory requirements of the method, the authors had to be quite creative and smart about how to encode changes in the network's weight changes.

There are tons of interesting experiments, which I encourage the reader to go check out (see section 3).

One experiment on training the learning rates, separately for each iteration (i.e. learning a learning rate schedule), for each layer and for either weights or biases (800 hyper-parameters total) shows that a good schedule is one where the top layer first learns quickly (large learning), then the bottom layer starts training faster, and finally the learning rates of all layers is decayed towards zero. Note that some of the experiments presented actually optimized the training error, instead of the validation set error.

Another looked at finding optimal scales for the weight initialization. Interestingly, the values found weren't that far from an often prescribed scale of $1 / \sqrt{N}$, where $N$ is the number of units in the previous layer.

The experiment on "training the training set", i.e. generating the 10 examples (one per class) that would minimize the validation set loss of a network trained on these examples is a pretty cool idea (it essentially learns prototypical images of the digits from 0 to 9 on MNIST).

Another experiment tried to optimize a multitask regularization matrix, in order to encourage forms of soft-weight-tying across tasks.

Note that approaches like the one in this paper make tools for automatic differentiation incredibly valuable. Python autograd, the author's automatic differentiation Python library https://github.com/HIPS/autograd (which inspired our own Torch autograd https://github.com/twitter/torch-autograd) was in fact developed in the context of this paper.

Finally, I'll end with a quote from the paper, that I found particularly funny: "The last remaining parameter to SGD is the initial parameter vector. Treating this vector as a hyperparameter blurs the distinction between learning and meta-learning. In the extreme case where all elementary learning rates are set to zero, the training set ceases to matter and the meta-learning procedure exactly reduces to elementary learning on the validation set. Due to philosophical vertigo, we chose not to optimize the initial parameter vector."

The paper introduces a sequential variational auto-encoder that generates complex images iteratively. The authors also introduce a new spatial attention mechanism that allows the model to focus on small subsets of the image. This new approach for image generation produces images that can’t be distinguished from the training data.

#### What is DRAW:
The deep recurrent attention writer (DRAW) model has two differences with respect to other variational auto-encoders. First, the encoder and the decoder are recurrent networks. Second, it includes an attention mechanism that restricts the input region observed by the encoder and the output region observed by the decoder.

#### What do we gain?
The resulting images are greatly improved by allowing a conditional and sequential generation. In addition, the spatial attention mechanism can be used in other contexts to solve the “Where to look?” problem.

#### What follows?
A possible extension to this model would be to use a convolutional architecture in the encoder or the decoder. Although this might be less useful since we are already restricting the input of the network.

#### Like:
* As observed in the samples generated by the model, the attention mechanism works effectively by reconstructing images in a local way.
* The attention model is fully differentiable.

#### Dislike:
* I think a better exposition of the attention mechanism would improve this paper.

A *Batch Normalization* applied immediately after fully connected layers and adjusts the values of the feedforward output so that they are centered to a zero mean and have unit variance.

It has been used by famous Convolutional Neural Networks such as GoogLeNet \cite{journals/corr/SzegedyLJSRAEVR14} and ResNet \cite{journals/corr/HeZRS15}