[link]
Summary by Alexander Jung 8 years ago
* They analyze the effects of using Batch Normalization (BN) and Weight Normalization (WN) in GANs (classical algorithm, like DCGAN).
* They introduce a new measure to rate the quality of the generated images over time.
### How
* They use BN as it is usually defined.
* They use WN with the following formulas:
* Strict weight-normalized layer:
* 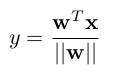
* Affine weight-normalized layer:
* 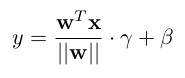
* As activation units they use Translated ReLUs (aka "threshold functions"):
* 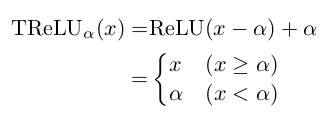
* `alpha` is a learned parameter.
* TReLUs play better with their WN layers than normal ReLUs.
* Reconstruction measure
* To evaluate the quality of the generated images during training, they introduce a new measure.
* The measure is based on a L2-Norm (MSE) between (1) a real image and (2) an image created by the generator that is as similar as possible to the real image.
* They generate (2) by starting `G(z)` with a noise vector `z` that is filled with zeros. The desired output is the real image. They compute a MSE between the generated and real image and backpropagate the result. Then they use the generated gradient to update `z`, while leaving the parameters of `G` unaltered. They repeat this for a defined number of steps.
* Note that the above described method is fairly time-consuming, so they don't do it often.
* Networks
* Their networks are fairly standard.
* Generator: Starts at 1024 filters, goes down to 64 (then 3 for the output). Upsampling via fractionally strided convs.
* Discriminator: Starts at 64 filters, goes to 1024 (then 1 for the output). Downsampling via strided convolutions.
* They test three variations of these networks:
* Vanilla: No normalization. PReLUs in both G and D.
* BN: BN in G and D, but not in the last layers and not in the first layer of D. PReLUs in both G and D.
* WN: Strict weight-normalized layers in G and D, except for the last layers, which are affine weight-normalized layers. TPReLUs (Translated PReLUs) in both G and D.
* Other
* They train with RMSProp and batch size 32.
### Results
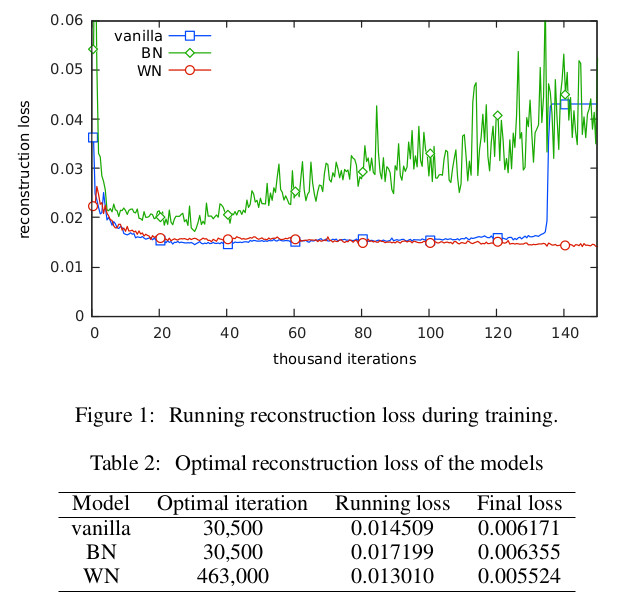
* Their WN formulation trains stable, provided the learning rate is set to 0.0002 or lower.
* They argue, that their achieved stability is similar to the one in WGAN.
* BN had significant swings in quality.
* Vanilla collapsed sooner or later.
* Both BN and Vanilla reached an optimal point shortly after the start of the training. After that, the quality of the generated images only worsened.
* Plot of their quality measure:
* 
* Their quality measure is based on reconstruction of input images. The below image shows examples for that reconstruction (each person: original image, vanilla reconstruction, BN rec., WN rec.).
* 
* Examples generated by their WN network:
* 














