TLDR; The authors present Residual Nets, which achieve 3.57% error on the ImageNet test set and won the 1st place on the ILSVRC 2015 challenge. ResNets work by introducing "shortcut" connections across stacks of layers, allowing the optimizer to learn an easier residual function instead of the original mapping. This allows for efficient training of very deep nets without the introduction of additional parameters or training complexity. The authors present results on ImageNet and CIFAR-100 with nets as deep as 152 layers (and one ~1000 layer deep net).


#### Key Points

- Problem: Deeper networks experience a *degradation* problem. They don't overfit but nonetheless perform worse than shallower networks on both training and test data due to being more difficult to optimize. 
- Because Deep Nets can in theory learn an identity mapping for their additional layers they should strict outperform shallower nets. In practice however, optimizers have problems learning identity (or near-identity) mappings. Learning residual mappings is easier, mitigating this problem.
- Residual Mapping: If the desired mapping is H(x), let the layers learn F(x) = H(x) - x and add x back through a shortcut connection H(x) = F(x) + x. An identity mapping can then be learned easily by driving the learned mapping F(x) to 0.
- No additional parameters or computational complexity are introduced by residuals nets.
- Similar to Highway Networks, but gates are not data-dependent (no extra parameters) and are always open.
- Due the the nature of the residual formula, input and output must be of same size (just like Highway Networks). We can do size transformation by zero-padding or projections. Projections introduce additional parameters. Authors found that projections perform slightly better, but are "not worth" the large number of extra parameters.
- 18 and 34-layer VGG-like plain net gets 27.94 and 28.54 error respectively, not that higher error for deeper net. ResNet gets 27.88 and 25.03 respectively. Error greatly reduces for deeper net.
- Use Bottleneck architecture with 1x1 convolutions to change dimensions.
- Single ResNet outperforms previous start of the art ensembles. ResNet ensemble even better.


#### Notes/Questions

- Love the simplicity of this.
- I wonder how performance depends on the number of layers skipped by the shortcut connections. The authors only present results with 2 or 3 layers.
- "Stacked" or recursive residuals?
- In principle Highway Networks should be able to learn the same mappings quite easily. Is this an optimization problem? Do we just not have enough data. What if we made the gates less fine-grained and substituted sigmoid with something else?
- Can we apply this to RNNs, similar to LSTM/GRU? Seems good for learning long-range dependencies.

This paper introduces Residual Nets (ResNets), which was the
winning submission (152-layer deep) at ILSVRC 2015 and MS-COCO 2015, and achieves
a top-5 error rate of 3.57% (ensemble of two  nets). Main contributions:

- The key idea is that deeper networks face the degradation problem, i.e.
higher training and test error than shallower nets, because they're harder
to optimize for approximating identity mapping by multiple non-linear layers.
    - They mitigate this problem by forcing solvers to learn residual functions
    i.e. $f(x) = H(x) - x$, by adding shortcut connections. If identity mapping is
    the optimal formulation, the learned weights should drive $f(x)$ to 0 (and they
    observe that this is a suitable preconditioning as most residual function responses
    are small).

- Shortcut connections (for identity mapping) don't require additional parameters.
    - Size transformations are done by zero-padding (no parameters) or projections. Projections
    introduce additional parameters and perform slightly better.

- Bottleneck design is used to further reduce computational complexity, i.e. 1x1 convolutional
layers before and after 3x3 convolutions to reduce and increase dimensions.

- For detection and localization tasks, they use ResNets in the Faster-RCNN setting.

## Strengths

- ResNets are significantly deeper and more accurate yet computationally cheaper than VGG.

- A single ResNet outperforms previous state-of-the-art ensembles. Their final winning submission
is an ensemble of two networks.

## Weaknesses / Notes

- The idea of shortcut connections to force blocks to learn residual functions preconditioned
on identity mapping is neat, and more so because it doesn't require additional parameters.

- A lot of results and design decisions merit further investigation and reasoning.
    - Why do shortcuts skip 2 or 3 layers? What happens to performance if we increase the number of layers skipped?
    - How well do shortcut connections work with Inception modules? The statistical principles
    underlying both these architectures seem to be orthogonal, does performance further improve?
    - 152 seems to be an arbitrary number of layers that 'worked'.

- The degradation problem seen when making networks deeper by initializing
layers with identity weight matrices seems to be contradictory to the results
presented in the Net2Net paper.

  * Deep plain/ordinary networks usually perform better than shallow networks.
  * However, when they get too deep their performance on the *training* set decreases. That should never happen and is a shortcoming of current optimizers.
  * If the "good" insights of the early layers could be transferred through the network unaltered, while changing/improving the "bad" insights, that effect might disappear.

###  What residual architectures are
  * Residual architectures use identity functions to transfer results from previous layers unaltered.
  * They change these previous results based on results from convolutional layers.
  * So while a plain network might do something like `output = convolution(image)`, a residual network will do `output = image + convolution(image)`.
  * If the convolution resorts to just doing nothing, that will make the result a lot worse in the plain network, but not alter it at all in the residual network.
  * So in the residual network, the convolution can focus fully on learning what positive changes it has to perform, while in the plain network it *first* has to learn the identity function and then what positive changes it can perform.

### How it works
  * Residual architectures can be implemented in most frameworks. You only need something like a split layer and an element-wise addition.
  * Use one branch with an identity function and one with 2 or more convolutions (1 is also possible, but seems to perform poorly). Merge them with the element-wise addition.
  * Rough example block (for a 64x32x32 input):
https://i.imgur.com/NJVb9hj.png  
  * An example block when you have to change the dimensionality (e.g. here from 64x32x32 to 128x32x32):
https://i.imgur.com/9NXvTjI.png
  * The authors seem to prefer using either two 3x3 convolutions or the chain of 1x1 then 3x3 then 1x1. They use the latter one for their very deep networks.
  * The authors also tested:
    * To use 1x1 convolutions instead of identity functions everywhere. Performed a bit better than using 1x1 only for dimensionality changes. However, also computation and memory demands.
    * To use zero-padding for dimensionality changes (no 1x1 convs, just fill the additional dimensions with zeros). Performed only a bit worse than 1x1 convs and a lot better than plain network architectures.
  * Pooling can be used as in plain networks. No special architectures are necessary.
  * Batch normalization can be used as usually (before nonlinearities).

### Results
  * Residual networks seem to perform generally better than similarly sized plain networks.
  * They seem to be able to achieve similar results with less computation.
  * They enable well-trainable very deep architectures with up to 1000 layers and more.
  * The activations of the residual layers are low compared to plain networks. That indicates that the residual networks indeed only learn to make "good" changes and default to "if in doubt, change nothing".


![Building blocks](https://raw.githubusercontent.com/aleju/papers/master/neural-nets/images/Deep_Residual_Learning_for_Image_Recognition__building_blocks.png?raw=true "Building blocks")

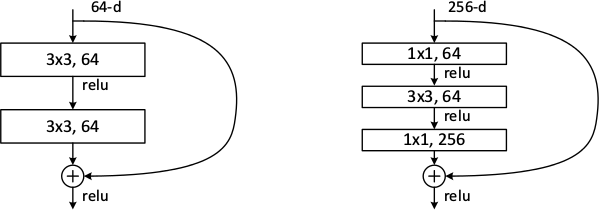
*Examples of basic building blocks (other architectures are possible). The paper doesn't discuss the placement of the ReLU (after add instead of after the layer).*


![Activations](https://raw.githubusercontent.com/aleju/papers/master/neural-nets/images/Deep_Residual_Learning_for_Image_Recognition__activations.png?raw=true "Activations")

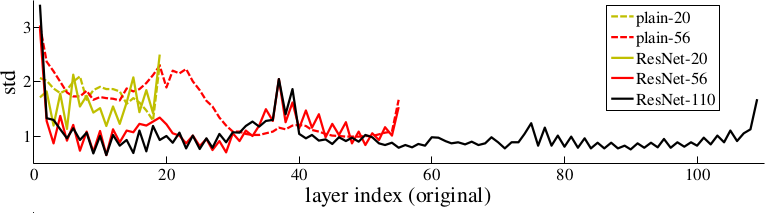
*Activations of layers (after batch normalization, before nonlinearity) throughout the network for plain and residual nets. Residual networks have on average lower activations.*

-------------------------

### Rough chapter-wise notes

* (1) Introduction
  * In classical architectures, adding more layers can cause the network to perform worse on the training set.
  * That shouldn't be the case. (E.g. a shallower could be trained and then get a few layers of identity functions on top of it to create a deep network.)
  * To combat that problem, they stack residual layers.
  * A residual layer is an identity function and can learn to add something on top of that.
  * So if `x` is an input image and `f(x)` is a convolution, they do something like `x + f(x)` or even `x + f(f(x))`.
  * The classical architecture would be more like `f(f(f(f(x))))`.
  * Residual architectures can be easily implemented in existing frameworks using skip connections with identity functions (split + merge).
  * Residual architecture outperformed other in ILSVRC 2015 and COCO 2015.

* (3) Deep Residual Learning
  * If some layers have to fit a function `H(x)` then they should also be able to fit `H(x) - x` (change between `x` and `H(x)`).
  * The latter case might be easier to learn than the former one.
  * The basic structure of a residual block is `y = x + F(x, W)`, where `x` is the input image, `y` is the output image (`x + change`) and `F(x, W)` is the residual subnetwork that estimates a good change of `x` (W are the subnetwork's weights).
  * `x` and `F(x, W)` are added using element-wise addition.
  * `x` and the output of `F(x, W)` must be have equal dimensions (channels, height, width).
  * If different dimensions are required (mainly change in number of channels) a linear projection `V` is applied to `x`: `y = F(x, W) + Vx`. They use a 1x1 convolution for `V` (without nonlinearity?).
  * `F(x, W)` subnetworks can contain any number of layer. They suggest 2+ convolutions. Using only 1 layer seems to be useless.
  * They run some tests on a network with 34 layers and compare to a 34 layer network without residual blocks and with VGG (19 layers).
  * They say that their architecture requires only 18% of the FLOPs of VGG. (Though a lot of that probably comes from VGG's 2x4096 fully connected layers? They don't use any fully connected layers, only convolutions.)
  * A critical part is the change in dimensionality (e.g. from 64 kernels to 128). They test (A) adding the new dimensions empty (padding), (B) using the mentioned linear projection with 1x1 convolutions and (C) using the same linear projection, but on all residual blocks (not only for dimensionality changes).
  * (A) doesn't add parameters, (B) does (i.e. breaks the pattern of using identity functions).
  * They use batch normalization before each nonlinearity.
  * Optimizer is SGD.
  * They don't use dropout.

* (4) Experiments
  * When testing on ImageNet an 18 layer plain (i.e. not residual) network has lower training set error than a deep 34 layer plain network.
  * They argue that this effect does probably not come from vanishing gradients, because they (a) checked the gradient norms and they looked healthy and (b) use batch normaliaztion.
  * They guess that deep plain networks might have exponentially low convergence rates.
  * For the residual architectures its the other way round. Stacking more layers improves the results.
  * The residual networks also perform better (in error %) than plain networks with the same number of parameters and layers. (Both for training and validation set.)
  * Regarding the previously mentioned handling of dimensionality changes:
    * (A) Pad new dimensions: Performs worst. (Still far better than plain network though.)
    * (B) Linear projections for dimensionality changes: Performs better than A.
    * (C) Linear projections for all residual blocks: Performs better than B. (Authors think that's due to introducing new parameters.)
  * They also test on very deep residual networks with 50 to 152 layers.
  * For these deep networks their residual block has the form `1x1 conv -> 3x3 conv -> 1x1 conv` (i.e. dimensionality reduction, convolution, dimensionality increase).
  * These deeper networks perform significantly better.
  * In further tests on CIFAR-10 they can observe that the activations of the convolutions in residual networks are lower than in plain networks.
  * So the residual networks default to doing nothing and only change (activate) when something needs to be changed.
  * They test a network with 1202 layers. It is still easily optimizable, but overfits the training set.
  * They also test on COCO and get significantly better results than a Faster-R-CNN+VGG implementation.

#### Goal:
+ Reformulate neural network architecture to address the degratation problem due to the very large number of layers.

#### Motivation:

![Motivation](https://raw.githubusercontent.com/tiagotvv/ml-papers/master/convolutional/images/He2015_motivation.png?raw=true "Motivation")

+ Degradation problem:
    + Increasing the depth of the network: accuracy gets saturated and then starts degrading.
    + As number of layers increase: higher training error.
    + In theory, such problem should not occur. Given a neural network, one can add new layers with identity mappings. In reality, optimization algorithms probably have difficulties to find (in feasible time)these solutions.


#### Residual Block:

+ Layers are reformulated as learning residual functions with reference to the layer inputs.

![Motivation](https://raw.githubusercontent.com/tiagotvv/ml-papers/master/convolutional/images/He2015_framework.png?raw=true "Motivation")

+ Residual Mapping. 
    + Neural networks with shortcut connections to perform identity mappings.
    + Identity shortcut connections do no add extra parameters or complexity to the network.
    + The problem can be seen as follows. Given the activation of layer L of a neural net, a[L], one can write the activation at layer L+2 as follows.

        a[L+2] = ReLu(W[L+2] * a[L+1] + b[L+2] + a[L])

    where W[L+2] is the weight matrix and b[L+2] is the bias vector at layer L+2.

    + The problem of learning an identity mapping is easier in this case, if weight decay is applied, W[L+2] goes to zero, as well as b[L+2].  The activation function at layer a[L+2] = ReLu(a[L]) = a[L].

    + One should take take to match the dimensions. A linear projection of the previous activation function could be used before the sum.


#### Datasets:

+ For the image classification task,  two datasets were used: ImageNet and CIFAR-10

|ImageNet|CIFAR-10
----|-----|-----
Training images | 1.2M | 50K
Validation images| 50K | (*)
Testing images | 100K | 10K
Number of classes | 1000 | 10

(*) in the experiments with CIFAR-10, the training images are split into 45K/5K training/validation sets.

#### Experiments and Results

**ImageNet Dataset**

+ Input images:
    + Scale jittering as in [Simonyan2015](https://github.com/tiagotvv/ml-papers/blob/master/convolutional/Very_Deep_Convolutional_Networks_for_Large_Scale_Image_Recognition.md). Image is resized with shorter size sampled to be in between [256, 480]. 
    + 224x224 crop from image is used.
    + Data augmentation following [Krizhevsky2012](https://github.com/tiagotvv/ml-papers/blob/master/convolutional/ImageNet_Classification_with_Deep_Convolutional_Neural_Networks.md) methodology: image flips, change RGB levels.
+ Training
    + Weight initialization: follows previous work by the authors.
    + Gradient descent with batch normalization, weight decay = 0.0001, momentum = 0.9
    + Mini-batch size = 256
    + Learning rate starts at 0.1 and is divided by 10 when accuracy stop increasing at the validation set.
    + Dropout is not employed
+ Testing
    + Multi-crop procedure from  [Krizhevsky2012](https://github.com/tiagotvv/ml-papers/blob/master/convolutional/ImageNet_Classification_with_Deep_Convolutional_Neural_Networks.md) is employed: 10 crops.
    + Fully connected layers are converted into convolutional layers.
    + Average of scores at multiple scales is employed. Testing scales used: {224, 256, 384, 480, 640}. 
+ Configurations tested on ImageNet dataset

 ![Motivation](https://raw.githubusercontent.com/tiagotvv/ml-papers/master/convolutional/images/He2015_architectures.png?raw=true "Motivation")

+ Single Model Results (validation set):

Architecture | top-1 error (%) | top-5 error (%)
----|:-----:|:-----:
VGG (ILSVRC'14) | - | 8.43
GoogLeNet (ILSVRC'14)  |-  | 7.89
VGG (v5) | 24.4 | 7.1
PReLU-net | 21.59 | 5.71
BN-inception | 21.99 | 5.81
ResNet-34 B (projections + identitites) | 21.84 | 5.71
ResNet-34 (projections) | 21.53 | 5.60
ResNet-50 | 20.74 | 5.25
ResNet-101| 19.87 | 4.60
ResNet-152 | **19.38** | **4.49**

+ Ensemble Models Results (test set):

Architecture | top-5 error (%)
----|:-----:|
VGG (ILSVRC'14) | 7.32 
GoogLeNet (ILSVRC'14)  | 6.66
VGG (v5) | 6.8
PReLU-net | 4.94 
BN-Inception | 4.82
ResNet (ILSVRC'15) | **3.57** 



**CIFAR-10 Dataset**

+ Input images:
    + Inputs: 32x32 images
    + Configurations tested on this dataset:
    
output map size | 32x32 | 16x16 | 8x8
----------------|-------|-------|----
num. layers | 1+2n | 2n | 2n
num. filters | 16 | 32 | 64

+ Shortcuts connected to pairs of 3x3 layers (3n shortcuts)  

+ Training
    + Weight initialization: follows previous work by the authors.
    + Gradient descent with batch normalization, weight decay = 0.0001, momentum = 0.9
    + Mini-batch size = 128, 2 GPUs.
    + Learning rate starts at 0.1 and is divided by 10 at 32k and 48k iterations. Stopped at 64k iterations.
    + Dropout is not employed
+ Testing
    + Single 32x32 image

+ Results

 ![CIFAR-10 results](https://raw.githubusercontent.com/tiagotvv/ml-papers/master/convolutional/images/He2015_CIFAR.png?raw=true "CIFAR-10 results")

Sources:
- https://arxiv.org/pdf/1512.03385.pdf
- http://image-net.org/challenges/talks/ilsvrc2015_deep_residual_learning_kaiminghe.pdf

Summary:
- Took the first place in Imagenet 5 main tracks
- Revolution of depth: GoogLeNet was 22 layers with 6.7 top-5 error, 
Resnet is 152 layers with 3.57 top-5 error
- Light on complexity: the 34 layer baseline is 18% of the FLOPs(multiply-adds) of VGG.
    - Resnet 152 has lower time complexity than VGG-16/19
- Extends well to detection and segmentation tasks
- Just stacking more layers gives worse performance. Why? In theory:
    > A deeper model should not have
    higher training error
    • A solution by construction:
    • original layers: copied from a
    learned shallower model
    • extra layers: set as identity
    • at least the same training error
    • Optimization difficulties: solvers
    cannot find the solution when going
    deeper…
- Why do the residual connections help? it's easier to learn a residual mapping w.r.t. identity. 
    - If identity were optimal, easy to set weights as 0
    - >If the optimal function is closer to an identity
mapping than to a zero mapping, it should be easier for the
solver to find the perturbations with reference to an identity
mapping, than to learn the function as a new one. We show
by experiments (Fig. 7) that the learned residual functions in
general have small responses, suggesting that identity mappings
provide reasonable preconditioning.
- Basic design (VGG-style)
    - all 3x3 conv (almost)
    - spatial size /2 => # filters x2
    - Simple design; just deep!
    - Other remarks:
        - no max pooling (almost)
        - no hidden fc
        - no dropout
- Training
    - All plain/residual nets are trained from scratch
    - All plain/residual nets use Batch Normalization
    - Standard hyper-parameters & augmentation
- The learned features are well transferable to other tasks
    - Works well with Faster RCNN
    - Works well with semantic instance segmentation
 
Also skimmed:
- Deep Residual Networks with 1K Layers
https://github.com/KaimingHe/resnet-1k-layers 
https://arxiv.org/pdf/1603.05027.pdf

_Objective:_ Solve the degradation problem where adding layers induces a higher training error.

_Dataset:_ [CIFAR10](https://www.cs.toronto.edu/%7Ekriz/cifar.html), [PASCAL](http://host.robots.ox.ac.uk/pascal/VOC/) and [COCO](http://mscoco.org/).

## Inner-workings:

They argue that it is easier to learn the difference to the identity (the residual) than the actual mapping. Basically they start with the identity and learn the residual mapping.  
This allows for easier training and thus deeper network.

## Architecture:

They introduce two new building block for Residual Networks, depending on the input dimensionality:  
[![screen shot 2017-05-31 at 3 49 59 pm](https://cloud.githubusercontent.com/assets/17261080/26635061/d489dbe2-4618-11e7-911e-68772265ee9f.png)](https://cloud.githubusercontent.com/assets/17261080/26635061/d489dbe2-4618-11e7-911e-68772265ee9f.png)  
[![screen shot 2017-05-31 at 3 57 47 pm](https://cloud.githubusercontent.com/assets/17261080/26635420/f6f22af8-4619-11e7-9639-ed651f8b18bb.png)](https://cloud.githubusercontent.com/assets/17261080/26635420/f6f22af8-4619-11e7-9639-ed651f8b18bb.png)

That can then be chained to produce network such as:  
[![screen shot 2017-05-31 at 3 54 16 pm](https://cloud.githubusercontent.com/assets/17261080/26635258/7b64530c-4619-11e7-81c8-5d6be547da77.png)](https://cloud.githubusercontent.com/assets/17261080/26635258/7b64530c-4619-11e7-81c8-5d6be547da77.png)

## Results:

Won most 1st places, very impressive and adding layers do increase accuracy.

This summary is as ridiculous as this network is long. A good implementation of the network is here: https://github.com/dmlc/mxnet/blob/master/example/image-classification/symbol_resnet-28-small.py


Here is a visualization of this crazy network:

![](http://josephpcohen.com/w/wp-content/uploads/resnet-28-small.png)