Identity Mappings in Deep Residual Networks
He, Kaiming and Zhang, Xiangyu and Ren, Shaoqing and Sun, Jian
European Conference on Computer Vision - 2016 via Local Bibsonomy
Keywords: dblp
He, Kaiming and Zhang, Xiangyu and Ren, Shaoqing and Sun, Jian
European Conference on Computer Vision - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
This is follow-up work to the ResNets paper. It studies the propagation formulations behind the connections of deep residual networks and performs ablation experiments. A residual block can be represented with the equations $y_l = h(x_l) + F(x_l, W_l); x_{l+1} = f(y_l)$. $x_l$ is the input to the l-th unit and $x_{l+1}$ is the output of the l-th unit. In the original ResNets paper, $h(x_l) = x_l$, $f$ is ReLu, and F consists of 2-3 convolutional layers (bottleneck architecture) with BN and ReLU in between. In this paper, they propose a residual block with both $h(x)$ and $f(x)$ as identity mappings, which trains faster and performs better than their earlier baseline. Main contributions:
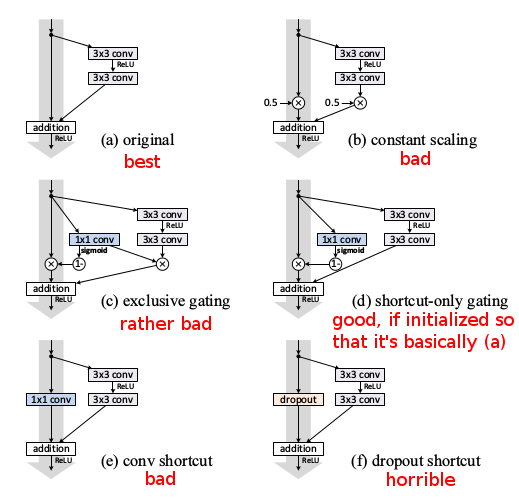
- Identity skip connections work much better than other multiplicative interactions that they experiment with:
- Scaling $(h(x) = \lambda x)$: Gradients can explode or vanish depending on whether modulating scalar \lambda > 1 or < 1.
- Gating ($1-g(x)$ for skip connection and $g(x)$ for function F):
For gradients to propagate freely, $g(x)$ should approach 1, but
F gets suppressed, hence suboptimal. This is similar to highway
networks. $g(x)$ is a 1x1 convolutional layer.
- Gating (shortcut-only): Setting high biases pushes initial $g(x)$
towards identity mapping, and test error is much closer to baseline.
- 1x1 convolutional shortcut: These work well for shallower networks
(~34 layers), but training error becomes high for deeper networks,
probably because they impede gradient propagation.
- Experiments on activations.
- BN after addition messes up information flow, and performs considerably
worse.
- ReLU before addition forces the signal to be non-negative, so the signal is monotonically increasing, while ideally a residual function should be free to take values in (-inf, inf).
- BN + ReLU pre-activation works best. This also prevents overfitting, due
to BN's regularizing effect. Input signals to all weight layers are normalized.
## Strengths
- Thorough set of experiments to show that identity shortcut connections
are easiest for the network to learn. Activation of any deeper unit can
be written as the sum of the activation of a shallower unit and a residual
function. This also implies that gradients can be directly propagated to
shallower units. This is in contrast to usual feedforward networks, where
gradients are essentially a series of matrix-vector products, that may vanish, as networks grow deeper.
- Improved accuracies than their previous ResNets paper.
## Weaknesses / Notes
- Residual units are useful and share the same core idea that worked in
LSTM units. Even though stacked non-linear layers are capable of asymptotically
approximating any arbitrary function, it is clear from recent work that
residual functions are much easier to approximate than the complete function.
The [latest Inception paper](http://arxiv.org/abs/1602.07261) also reports
that training is accelerated and performance is improved by using identity
skip connections across Inception modules.
- It seems like the degradation problem, which serves as motivation for
residual units, exists in the first place for non-idempotent activation
functions such as sigmoid, hyperbolic tan. This merits further
investigation, especially with recent work on function-preserving transformations such as [Network Morphism](http://arxiv.org/abs/1603.01670), which expands the Net2Net idea to sigmoid, tanh, by using parameterized activations, initialized to identity mappings.

Your comment:
|
|
[link]
* The authors reevaluate the original residual design of neural networks.
* They compare various architectures of residual units and actually find one that works quite a bit better.
### How
* The new variation starts the transformation branch of each residual unit with BN and a ReLU.
* It removes BN and ReLU after the last convolution.
* As a result, the information from previous layers can flow completely unaltered through the shortcut branch of each residual unit.
* The image below shows some variations (of the position of BN and ReLU) that they tested. The new and better design is on the right:
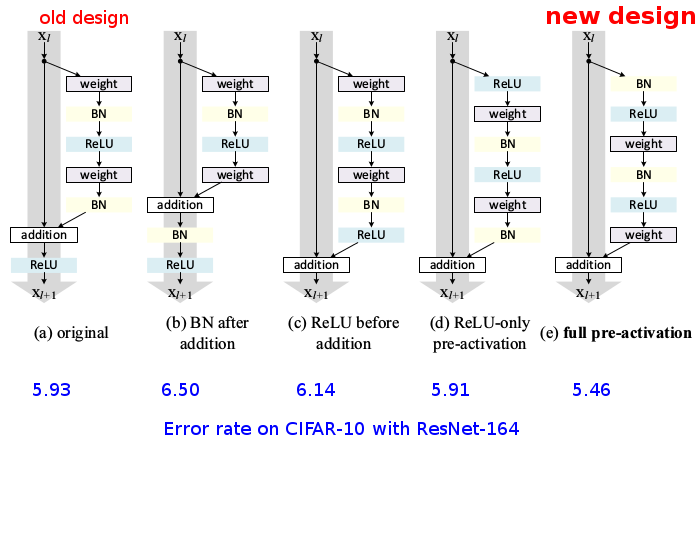
* They also tried various alternative designs for the shortcut connections. However, all of these designs performed worse than the original one. Only one (d) came close under certain conditions. Therefore, the recommendation is to stick with the old/original design.
### Results
* Significantly faster training for very deep residual networks (1001 layers).
* Better regularization due to the placement of BN.
* CIFAR-10 and CIFAR-100 results, old vs. new design:
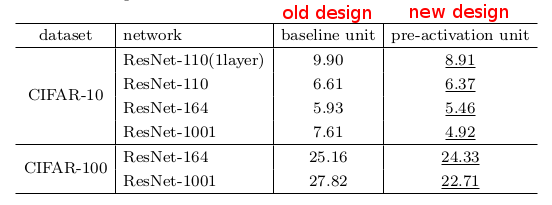
 |
You must log in before you can submit this summary! Your draft will not be saved!
Preview:












