_Objective:_ Build a network easily trainable by back-propagation to perform unsupervised domain adaptation while at the same time learning a good embedding for both source and target domains.

_Dataset:_ [SVHN](ufldl.stanford.edu/housenumbers/), [MNIST](yann.lecun.com/exdb/mnist/), [USPS](https://www.otexts.org/1577), [CIFAR](https://www.cs.toronto.edu/%7Ekriz/cifar.html) and [STL](https://cs.stanford.edu/%7Eacoates/stl10/).


## Architecture:

Very similar to RevGrad but with some differences.

Basically a shared encoder and then a classifier and a reconstructor.  
[![screen shot 2017-05-22 at 6 11 22 pm](https://cloud.githubusercontent.com/assets/17261080/26318076/21361592-3f1a-11e7-9213-9cc07cfe2f2a.png)](https://cloud.githubusercontent.com/assets/17261080/26318076/21361592-3f1a-11e7-9213-9cc07cfe2f2a.png)

The two losses are:

*   the usual cross-entropy with softmax for the classifier
*   the pixel-wise squared loss for reconstruction

Which are then combined using a trade-off hyper-parameter between classification and reconstruction.

They also use data augmentation to generate additional training data during the supervised training using only geometrical deformation: translation, rotation, skewing, and scaling

Plus denoising to reconstruct clean inputs given their noisy counterparts (zero-masked noise and Gaussian noise).

## Results:

Outperforms state of the art on most tasks at the time, now outperformed itself by Generate To Adapt on most tasks.

  * They describe a convolutional network that takes in photos and returns where (on the planet) these photos were likely made.
  * The output is a distribution over locations around the world (so not just one single location). This can be useful in the case of ambiguous images.

### How
  * Basic architecture
    * They simply use the Inception architecture for their model.
    * They have 97M parameters.
  * Grid
    * The network uses a grid of cells over the planet.
    * For each photo and every grid cell it returns the likelihood that the photo was made within the region covered by the cell (simple softmax layer).
    * The naive way would be to use a regular grid around the planet (i.e. a grid in which all cells have the same size).
      * Possible disadvantages:
        * In places where lots of photos are taken you still have the same grid cell size as in places where barely any photos are taken.
        * Maps are often distorted towards the poles (countries are represented much larger than they really are). This will likely affect the grid cells too.
    * They instead use an adaptive grid pattern based on S2 cells.
      * S2 cells interpret the planet as a sphere and project a cube onto it.
      * The 6 sides of the cube are then partitioned using quad trees, creating the grid cells.
      * They don't use the same depth for all quad trees. Instead they subdivide them only if their leafs contain enough photos (based on their dataset of geolocated images).
      * They remove some cells for which their dataset does not contain enough images, e.g. cells on oceans. (They also remove these images from the dataset. They don't say how many images are affected by this.)
      * They end up with roughly 26k cells, some of them reaching the street level of major cities.
      * Visualization of their cells:
        ![S2 cells](https://raw.githubusercontent.com/aleju/papers/master/neural-nets/images/PlaNet__S2.jpg?raw=true "S2 cells")
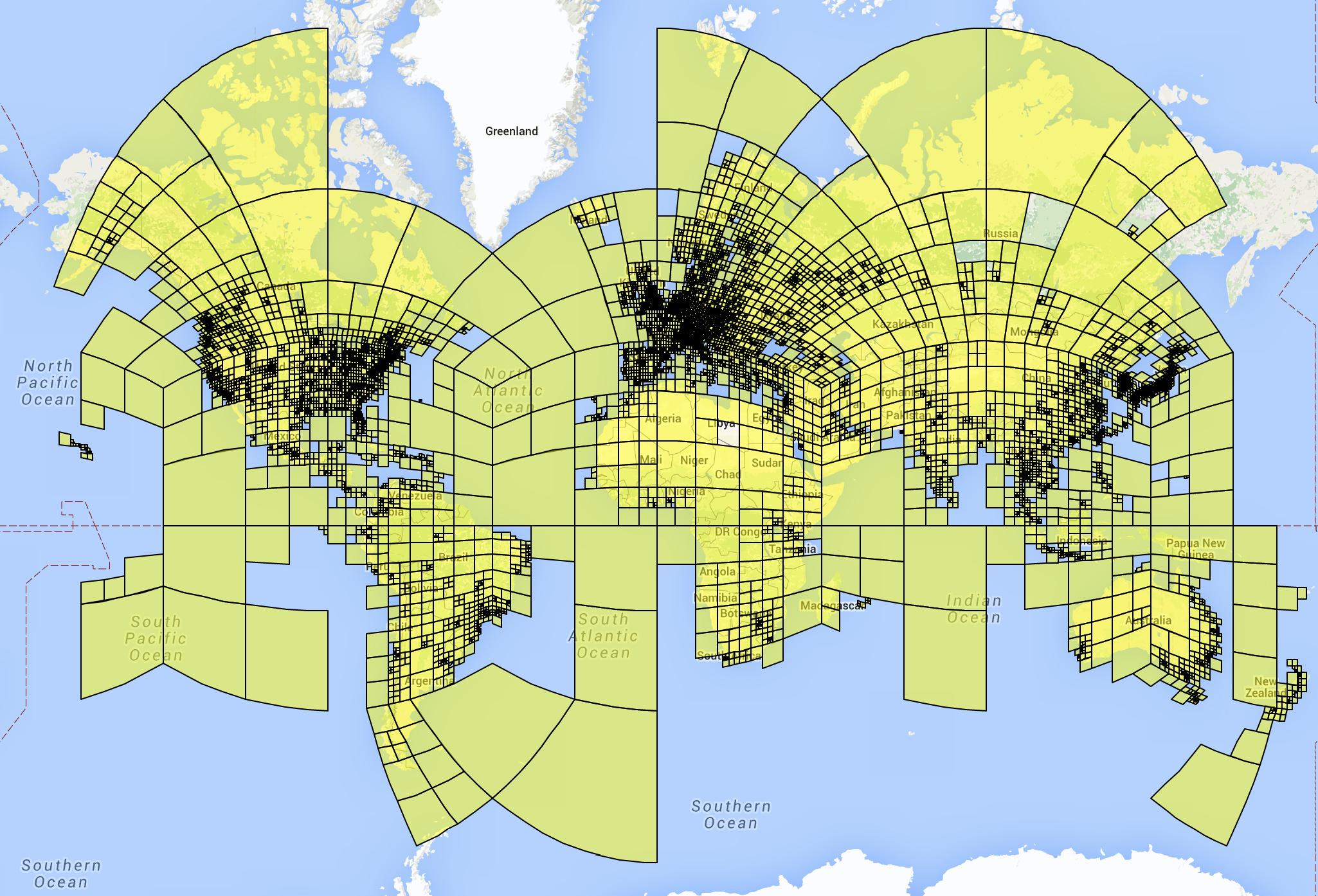
  * Training
    * For each example photo that they feed into the network, they set the correct grid cell to `1.0` and all other grid cells to `0.0`.
    * They train on a dataset of 126M images with Exif geolocation information. The images were collected from all over the web.
    * They used Adagrad.
    * They trained on 200 CPUs for 2.5 months.
  * Album network
    * For photo albums they develop variations of their network.
    * They do that because albums often contain images that are very hard to geolocate on their own, but much easier if the other images of the album are seen.
    * They use LSTMs for their album network.
    * The simplest one just iterates over every photo, applies their previously described model to it and extracts the last layer (before output) from that model. These vectors (one per image) are then fed into an LSTM, which is trained to predict (again) the grid cell location per image.
    * More complicated versions use multiple passes or are bidirectional LSTMs (to use the information from the last images to classify the first ones in the album).

### Results
  * They beat previous models (based on hand-engineered features or nearest neighbour methods) by a significant margin.
  * In a small experiment they can beat experienced humans in geoguessr.com.
  * Based on a dataset of 2.3M photos from Flickr, their method correctly predicts the country where the photo was made in 30% of all cases (top-1; top-5: about 50%). City-level accuracy is about 10% (top-1; top-5: about 18%).
  * Example predictions (using in coarser grid with 354 cells):
    ![Examples](https://raw.githubusercontent.com/aleju/papers/master/neural-nets/images/PlaNet__examples.png?raw=true "Examples")
  * Using the LSTM-technique for albums significantly improves prediction accuracy for these images.

https://www.youtube.com/watch?v=PRD8LpPvdHI

  * They describe a method that can be used for two problems:
    * (1) Choose a style image and apply that style to other images.
    * (2) Choose an example texture image and create new texture images that look similar.
  * In contrast to previous methods their method can be applied very fast to images (style transfer) or noise (texture creation). However, per style/texture a single (expensive) initial training session is still necessary.
  * Their method builds upon their previous paper "Combining Markov Random Fields and Convolutional Neural Networks for Image Synthesis".

### How
  * Rough overview of their previous method:
    * Transfer styles using three losses:
      * Content loss: MSE between VGG representations.
      * Regularization loss: Sum of x-gradient and y-gradients (encouraging smooth areas).
      * MRF-based style loss: Sample `k x k` patches from VGG representations of content image and style image. For each patch from content image find the nearest neighbor (based on normalized cross correlation) from style patches. Loss is then the sum of squared errors of euclidean distances between content patches and their nearest neighbors.
    * Generation of new images is done by starting with noise and then iteratively applying changes that minimize the loss function.
  * They introduce mostly two major changes:
    * (a) Get rid of the costly nearest neighbor search for the MRF loss. Instead, use a discriminator-network that receives a patch and rates how real that patch looks.
      * This discriminator-network is costly to train, but that only has to be done once (per style/texture).
    * (b) Get rid of the slow, iterative generation of images. Instead, start with the content image (style transfer) or noise image (texture generation) and feed that through a single generator-network to create the output image (with transfered style or generated texture).
      * This generator-network is costly to train, but that only has to be done once (per style/texture). 
  * MDANs
    * They implement change (a) to the standard architecture and call that an "MDAN" (Markovian Deconvolutional Adversarial Networks).
    * So the architecture of the MDAN is:
      * Input: Image (RGB pixels)
      * Branch 1: Markovian Patch Quality Rater (aka Discriminator)
        * Starts by feeding the image through VGG19 until layer `relu3_1`. (Note: VGG weights are fixed/not trained.)
        * Then extracts `k x k` patches from the generated representations.
        * Feeds each patch through a shallow ConvNet (convolution with BN then fully connected layer).
        * Training loss is a hinge loss, i.e. max margin between classes +1 (real looking patch) and -1 (fake looking patch). (Could also take a single sigmoid output, but they argue that hinge loss isn't as likely to saturate.)
        * This branch will be trained continuously while synthesizing a new image.
      * Branch 2: Content Estimation/Guidance
        * Note: This branch is only used for style transfer, i.e if using an content image and not for texture generation.
        * Starts by feeding the currently synthesized image through VGG19 until layer `relu5_1`. (Note: VGG weights are fixed/not trained.)
        * Also feeds the content image through VGG19 until layer `relu5_1`.
        * Then uses a MSE loss between both representations (so similar to a MSE on RGB pixels that is often used in autoencoders).
        * Nothing in this branch needs to trained, the loss only affects the synthesizing of the image.
  * MGANs
    * The MGAN is like the MDAN, but additionally implements change (b), i.e. they add a generator that takes an image and stylizes it.
    * The generator's architecture is:
      * Input: Image (RGB pixels) or noise (for texture synthesis)
      * Output: Image (RGB pixels) (stylized input image or generated texture)
      * The generator takes the image (pixels) and feeds that through VGG19 until layer `relu4_1`.
      * Similar to the DCGAN generator, they then apply a few fractionally strided convolutions (with BN and LeakyReLUs) to that, ending in a Tanh output. (Fractionally strided convolutions increase the height/width of the images, here to compensate the VGG pooling layers.)
      * The output after the Tanh is the output image (RGB pixels).
    * They train the generator with pairs of `(input image, stylized image or texture)`. These pairs can be gathered by first running the MDAN alone on several images. (With significant augmentation a few dozen pairs already seem to be enough.)
    * One of two possible loss functions can then be used:
      * Simple standard choice: MSE on the euclidean distance between expected output pixels and generated output pixels. Can cause blurriness.
      * Better choice: MSE on a higher VGG representation. Simply feed the generated output pixels through VGG19 until `relu4_1` and the reuse the already generated (see above) VGG-representation of the input image. This is very similar to the pixel-wise comparison, but tends to cause less blurriness.
    * Note: For some reason the authors call their generator a VAE, but don't mention any typical VAE technique, so it's not described like one here.
  * They use Adam to train their networks.
  * For texture generation they use Perlin Noise instead of simple white noise. In Perlin Noise, lower frequency components dominate more than higher frequency components. White noise didn't work well with the VGG representations in the generator (activations were close to zero).

### Results
  * Similar quality like previous methods, but much faster (compared to most methods).
  * For the Markovian Patch Quality Rater (MDAN branch 1):
    * They found that the weights of this branch can be used as initialization for other training sessions (e.g. other texture styles), leading to a decrease in required iterations/epochs.
    * Using VGG for feature extraction seems to be crucial. Training from scratch generated in worse results.
    * Using larger patch sizes preserves more structure of the structure of the style image/texture. Smaller patches leads to more flexibility in generated patterns.
    * They found that using more than 3 convolutional layers or more than 64 filters per layer provided no visible benefit in quality.


![Example](https://raw.githubusercontent.com/aleju/papers/master/neural-nets/images/Markovian_GANs__example.png?raw=true "Example")

*Result of their method, compared to other methods.*


![Architecture](https://raw.githubusercontent.com/aleju/papers/master/neural-nets/images/Markovian_GANs__architecture.png?raw=true "Architecture")

*Architecture of their model.*

In this paper, the authors present a new measure for evaluating person tracking performance and to overcome problems when using other event-based measures (MOTA - Multi Object Tracking Accuracy, MCTA - Multi Camera Tracking Accuracy, Handover error) in multi-camera scenario. 
The emphasis is on maintaining correct ID for a trajectory in most frames instead of penalizing identity switches. This way, the proposed measure is suitable for MTMC (Multi-target Multi-camera) setting where the tracker is agnostic to the true identities. 

They do not claim that one measure is better than the other, but each one serves a different purpose. For applications where preserving identity is important, it is fundamental to have measures (like the proposed ID precision and ID recall) which evaluate how well computed identities conform to true identities, while disregarding where or why mistakes occur. More formally, the new pair of precision-recall measures ($IDP$ and $IDR$), and the corresponding $F_1$ score $IDF_1$ are formulated as:
\begin{equation}
IDP = \dfrac{IDTP}{IDTP+IDFP}
\end{equation}

\begin{equation}
IDR = \dfrac{IDTP}{IDTP+IDFN}
\end{equation}

\begin{equation}
IDF_1 = \dfrac{2 \times IDTP}{2 \times IDTP + IDFP + IDFN}
\end{equation}

where $IDTP$ is the True Positive ID, $IDFP$ is the False Positive ID, and $IDFN$ is the False Negative ID for every corresponding association. 

Another contribution of the paper is a large fully-annotated dataset recorded in an outdoor environment. Details of the dataset: It has more than $2$ million frames of high resolution $1080$p,$60$fps  video,  observing more than $2700$ identities and includes surveillance footage from $8$ cameras with approximately $85$ minutes of videos for each camera. The dataset is available here: http://vision.cs.duke.edu/DukeMTMC/. 

Experiments show that the performance of their reference tracking system on another dataset (http://mct.idealtest.org/Datasets.html), when evaluated with existing measures, is comparable to other MTMC trackers. Also, a baseline framework on their data is established for future comparisons. 

This paper deals with an important problem where a deep classification system is made explainable. After the (continuing) success of Deep Networks, researchers are trying to open the blackbox and this work is one of the foremosts. The authors explored the strength of a deep learning method (vision-language model) to explain the performance of another deep learning model (image classification). The approach jointly predicts a class label and explains why it predicted so in natural language.

The paper starts with a very important differentiation between two basic schools of *explnation* systems - the *introspection* explanation system and the *justification* explanation system. The introspection system looks into the model to get an explanation (e.g., "This is a Western Grebe because filter 2 has a high activation..."). On the other hand, a justification system justifies the decision by producing sentence details on how visual evidence is compatible with the system output (e.g., "This is a Western Grebe because it has red eyes..."). The paper focuses on *justification* explanation system and proposes a novel one.

The authors argue that unlike a description of an image or a sentence defining a class (not necessarily in presence of an image), visual explanation, conditioned on an input image, provides much more of an explanatory text on why the image is classified as a certain category mentioning only image relevant features. The broad outline of the approach is given in Fig (2) of the paper.
https://i.imgur.com/tta2qDp.png
The first stage consists of a deep convolutional network for classification which generates a softmax distribution over the classes. As the task handles fine-grained bird species classification, it uses a compact bilinear feature representation known to work well for the fine-grained classification tasks. The second stage is a stacked LSTM which generates natural language sentences or explanations justifying the decision of the first stage. The first LSTM of the stack receives the previously generated word. The second LSTM receives the output of the first LSTM along with image features and predicted label distribution from the classification network. This LSTM produces the sequence of output words until an "end-of-sentence" token is generated. The intuition behind using predicted label distribution for explanation is that it would inform the explanation generation model which words and attributes are more likely to occur in the description.

Two kinds of losses are used for the second stage *i.e.*, the language model. The first one is termed as the *Relevance Loss* which is the typical sentence generation loss that is seen in literature. This is the sum of cross-entropy losses of the generated words with respect to the ground truth words. Its role is to optimize the alignment between generated and ground truth sentences. However, this loss is not very effective in producing sentences which include class discriminative information. class specificity is a global sentence property. This is illustrated with the following example - *whereas a sentence "This is an all black bird with a bright red eye" is class specific to a "Bronzed Cowbird", words and phrases in the sentence, such as "black" or "red eye" are less class discriminative on their own.* As a result, cross entropy loss on individual words turns out to be less effective in capturing the global sentence property of which class specifity is an example. The authors address this issue by proposing an addiitonal loss, termed as the *Discriminative Loss* which is based on a reinforcement learning paradigm. Before computing the loss, a sentence is sampled. The sentence is passed through a LSTM-based classification network whose task is to produce the ground truth category $C$ given only the sampled sentence. The reward for this operation is simply the probability of the ground truth category $C$ given only the sentence. The intuition is - for the model to produce an output with a large reward, the generated sentence must include enough information to classify the original image properly. The *Discriminative Loss* is the expectation of the negative of this reward and a wieghted linear combination of the two losses is optimized during training.

My experience in reinforcement learning is limited. However, I must say I did not quite get why is sampling of the sentences required (which called for the special algorithm for backpropagation). If the idea is to see whether a generated sentence can be used to get at the ground truth category, could the last internal state of one of the stacked LSTM not be used? It would have been better to get some more intution behind the sampling operation. Another thing which (is fairly obvious but still I felt) is missing is not mentioning the loss used in the fine grained classification network.

The experimentation is rigorous. The proposed method is compared with four different baseline and ablation models - description, definition, explanation-label, explanation-discriminative with different permutation and combinations of the presence of two types losses, class precition informations etc. Also the evaluation metrics measure different qualities of the generated exlanations, specifically image and class relevances. To measure image relevance METEOR/CIDEr scores of the generated sentences with the ground truth (image based) explanations are computed. On the other hand, to measure the class relevance, CIDEr scores with class definition (not necessarily based on the images from the dataset) sentences are computed. The proposed approach has continuously shown better performance than any of the baseline or ablation methods. I'd specifically mention about one experiment where the effect of class conditioning is studies (end of Sec 5.2). The finding is quite interesting as it shows that providing or not providing correct class information has drastic effect at the generated explanations. It is seen that giving incorrect class information makes the explanation model hallucinate colors or attributes which are not present in the image but are specific to the class. This raises the question whether it is worth giving the class information when the classifier is poor on the first hand? But, I think the answer lies in the observation that row 5 (with class prediction information) in table 1 is always better than row 4 (no class prediction information). Since, row 5 is better than row 4, this means the classifier is also reasonable and this in turn implies that end-to-end training can improve all the stages of a pipeline which ultimately improves the overall performance of the system too!

In summary, the paper is a very good first step to explain intelligent systems and should encourage a lot more effort in this direction.

This is follow-up work to the ResNets paper. It studies the propagation formulations behind the connections of deep residual networks and performs ablation experiments. A residual block can be represented with the equations $y_l = h(x_l) + F(x_l, W_l); x_{l+1} = f(y_l)$. $x_l$ is the input to the l-th unit and $x_{l+1}$ is the output of the l-th unit. In the original ResNets paper, $h(x_l) = x_l$, $f$ is ReLu, and F consists of 2-3 convolutional layers (bottleneck architecture) with BN and ReLU in between. In this paper, they propose a residual block with both $h(x)$ and $f(x)$ as identity mappings, which trains faster and performs better than their earlier baseline. Main contributions:

- Identity skip connections work much better than other multiplicative interactions that they experiment with:
    - Scaling $(h(x) = \lambda x)$: Gradients can explode or vanish depending on whether modulating scalar \lambda > 1 or < 1.
    - Gating ($1-g(x)$ for skip connection and $g(x)$ for function F):
    For gradients to propagate freely, $g(x)$ should approach 1, but
    F gets suppressed, hence suboptimal. This is similar to highway
    networks. $g(x)$ is a 1x1 convolutional layer.
    - Gating (shortcut-only): Setting high biases pushes initial $g(x)$
    towards identity mapping, and test error is much closer to baseline.
    - 1x1 convolutional shortcut: These work well for shallower networks
    (~34 layers), but training error becomes high for deeper networks,
    probably because they impede gradient propagation.

- Experiments on activations.
    - BN after addition messes up information flow, and performs considerably
    worse.
    - ReLU before addition forces the signal to be non-negative, so the signal is monotonically increasing, while ideally a residual function should be free to take values in (-inf, inf).
    - BN + ReLU pre-activation works best. This also prevents overfitting, due
    to BN's regularizing effect. Input signals to all weight layers are normalized.

## Strengths

- Thorough set of experiments to show that identity shortcut connections
are easiest for the network to learn. Activation of any deeper unit can
be written as the sum of the activation of a shallower unit and a residual
function. This also implies that gradients can be directly propagated to
shallower units. This is in contrast to usual feedforward networks, where
gradients are essentially a series of matrix-vector products, that may vanish, as networks grow deeper.

- Improved accuracies than their previous ResNets paper.

## Weaknesses / Notes

- Residual units are useful and share the same core idea that worked in
LSTM units. Even though stacked non-linear layers are capable of asymptotically
approximating any arbitrary function, it is clear from recent work that
residual functions are much easier to approximate than the complete function.
The [latest Inception paper](http://arxiv.org/abs/1602.07261) also reports
that training is accelerated and performance is improved by using identity
skip connections across Inception modules.

- It seems like the degradation problem, which serves as motivation for
residual units, exists in the first place for non-idempotent activation
functions such as sigmoid, hyperbolic tan. This merits further
investigation, especially with recent work on function-preserving transformations such as [Network Morphism](http://arxiv.org/abs/1603.01670), which expands the Net2Net idea to sigmoid, tanh, by using parameterized activations, initialized to identity mappings.

This paper proposes the use of pretrained convolutional neural networks that have already learned to encode semantic information as loss functions for training networks for style transfer and super-resolution. The trained networks corresponding to selected style images are capable of performing style transfer for any content image with a single forward pass (as opposed to explicit optimization over output image) achieving as high as 1000x speedup and similar qualitative results as Gatys et al. Key contributions:

- Image transformation network
    - Convolutional neural network with residual blocks and strided & fractionally-strided convolutions for in-network downsampling and upsampling. 
    - Output is the same size as input image, but rather than training the network with a per-pixel loss, it is trained with a feature reconstruction perceptual loss.

- Loss network
    - VGG-16 with frozen weights 
    - Feature reconstruction loss: Euclidean distance between feature representations
    - Style reconstruction loss: Frobenius norm of the difference between Gram matrices, performed over a set of layers.

- Experiments
    - Similar objective values and qualitative results as explicit optimization over image as in Gatys et al for style transfer
    - For single-image super-resolution, feature reconstruction loss reconstructs fine details better and 'looks' better than a per-pixel loss, even though PSNR values indicate otherwise. Respectable results in comparison to SRCNN.

## Weaknesses / Notes

- Although fast, limited by styles at test-time (as opposed to iterative optimizer that is limited by speed and not styles). Ideally, there should be a way to feed in style and content images, and do style transfer with a single forward pass.

Problem
----------
Given an unconstrained image, estimate:
1. 3d pose of human skeleton 
2. 3d body mesh


Contributions
-----------
1. full body mesh extraction from image
2. improvement of state of the art


Datasets
-------------
1. Leeds Sports
2. HumanEva
3. Human3.6M


Approach
----------------
Consider the problem both bottom-up and top-down.
1. Bottom-up: DeepCut cnn model to fit joints 2d positions onto the image.
2. top-down: A skinned multi-person linear model (SMPL) is fitted and projected onto 2d joint positions and image.

SSD aims to solve the major problem with most of the current state of the art object detectors namely Faster RCNN and like. All the object detection algortihms have same  methodology 

- Train 2 different nets - Region Proposal Net (RPN) and advanced classifier to detect class of an object and bounding box separately.
- During inference, run the test image at different scales to detect object at multiple scales to account for invariance

This makes the nets extremely slow. Faster RCNN could operate at **7 FPS with 73.2% mAP** while SSD could achieve **59 FPS with 74.3% mAP ** on VOC 2007 dataset.

#### Methodology

SSD uses a single net for predict object class and bounding box. However it doesn't do that directly. It uses a mechanism for choosing ROIs, training end-to-end for predicting class and boundary shift for that ROI.

##### ROI selection

Borrowing from FasterRCNNs SSD uses the  concept of anchor boxes for generating ROIs from the feature maps of last layer of shared conv layer. For each pixel in layer of feature maps, k default boxes with different aspect ratios are chosen around every pixel in the map. So if there are feature maps each of m x n resolutions - that's *mnk* ROIs for a single feature layer. Now SSD uses multiple feature layers (with differing resolutions) for generating such ROIs primarily to capture size invariance of objects. But because earlier layers in deep conv net tends to capture low level features, it uses features after certain levels and layers henceforth.

##### ROI labelling
Any ROI that matches to Ground Truth for a class after applying appropriate transforms and having Jaccard overlap greater than 0.5 is positive. Now, given all feature maps are at different resolutions and each boxes are at different aspect ratios, doing that's not simple. SDD uses simple scaling and aspect ratios to get to the appropriate  ground truth dimensions for calculating Jaccard overlap for default boxes for each pixel at the given resolution

##### ROI classification

SSD uses single convolution kernel of 3*3 receptive fields to predict for each ROI the 4 offsets (centre-x offset, centre-y offset, height offset , width offset) from the Ground Truth box for each RoI, along with class confidence scores for each class. So that is if there are c classes (including background), there are (c+4) filters for each convolution kernels that looks at a ROI. 

So summarily we have convolution kernels  that look at ROIs (which are default boxes around each pixel in feature map layer) to generate (c+4) scores for each RoI. Multiple feature map layers with different resolutions are used for generating such ROIs. Some ROIs are positive and some negative depending on jaccard overlap after ground box has scaled appropriately taking resolution differences in input image and feature map into consideration.

Here's how it looks :
![](https://i.imgur.com/HOhsPZh.png)

##### Training

For each ROI a combined loss is calculated as a combination of localisation error and classification error. The details are best explained in the figure. 
![](https://i.imgur.com/zEDuSgi.png)

##### Inference
For each ROI predictions a small threshold is used to first filter out irrelevant predictions, Non Maximum Suppression (nms) with jaccard overlap of 0.45 per class is applied then on the remaining candidate ROIs and the top 200 detections per image are kept.

For further understanding of the intuitions regarding the paper and the results obtained please consider giving the full paper a read. 

The open sourced code is available at this [Github repo](https://github.com/weiliu89/caffe/tree/ssd)
 

This paper introduces a bunch of tricks which make sense for visual tracking. These tricks are as followed:
1. At test time, a crop with center at the previous frame's bounding box's center with size larger than the bounding box is given along with the search area in the current frame.
2. Training offline on a large set of videos (where object bounding boxes are given for a subset of frames) and images with object bounding boxes.
3. Network takes two images: i) a crop of the image/frame around the bounding box and  ii) the image centered at the center of the bounding box. Given the later, network regresses the bounding box in i).
4. Above crops are sampled such that the ground truth bounding box center in i) is not very far from the center in ii), hence network prefers smooth motion.

My take: This is very nice way to use still images to train image correlation task and hence can be used for tracking. Speed on gpu is very impressive but still not comparable on CPUs.

The core idea behind this paper is powerfully simple. The goal is to learn useful representations from unlabelled data, useful in the sense of helping supervised object classification. This paper does this by chopping up images into a set of little jigsaw puzzle, scrambling the pieces, and asking a deep neural network to learn to reassemble them in the correct constellation. A picture is worth a thousand words, so here is Figure 1 taken from the paper explaining this visually:

![](http://www.inference.vc/content/images/2016/04/Screen-Shot-2016-04-25-at-08-26-45-1.png)

#### Summary of this note:

- I note the similarities to denoising autoencoders, which motivate my question: "Can this method equivalently represent the data generating distribution?"
- I consider a toy example with just two jigsaw pieces, and consider using an objective like this to fit a generative model $Q$ to data
- I show how the jigsaw puzzle training procedure corresponds to minimising a difference of KL divergences
- Conclude that the algorithm ignores some aspects of the data generating distribution, and argue that in this case it can be a good thing

#### What does this learn do?

This idea seems to make a lot of sense. But to me, one interesting question is the following:

`What does a network trained to solve jigsaw puzzle learn about the data generating distribution?`

#### Motivating example: denoising autoencoders

At one level, this jigsaw puzzle approach bears similarities to denoising autoencoders (DAEs): both methods are self-supervised: they take an unlabelled data and generate a synthetic supervised learning task. You can also interpret solving jigsaw puzzles as a special case 'undoing corruption' thus fitting a more general definition of autoencoders (Bengio et al, 2014).

DAEs have been shown to be related to score matching (Vincent, 2000), and that they learn to represent gradients of the log-probability-density-function of the data generating distribution (Alain et al, 2012). In this sense, autoencoders equivalently represent a complete probability distribution up to normalisation. This concept is also exploited in Harri Valpola's work on ladder networks (Rasmus et al, 2015)

So I was curious if I can find a similar neat interpretation of what really is going on in this jigsaw puzzle thing. If you equivalently represent all aspects of a probability distribution this way? Are there aspects that this representation ignores? Would it correspond to a consistent denisty estimation/generative modelling method in any sense? Below is my attempt to figure this out.

#### A toy case with just two jigsaw pieces

To simplify things, let's just consider a simpler jigsaw puzzle problem with just two jigsaw positions instead of 9, and in such a way that there are no gaps between puzzle pieces, so image patches (now on referred to as data $x$) can be partitioned exactly into pieces.

Let's assume our datapoints $x^{(n)}$ are drawn i.i.d. from an unknown distribution $P$, and that $x$ can be partitioned into two chunks $x_1$ and $x_2$ of equivalent dimensionality, such that $x=(x_1,x_2)$ by definition. Let's also define the permuted/scrambled version of a datapoint $x$ as $\hat{x}:=(x_2,x_1)$.

The jigsaw puzzle problem can be formulated in the following way: we draw a datapoint $x$ from $P$. We also independently draw a binary 'label' $y$ from a Bernoulli($\frac{1}{2}$) distribution, i.e. toss a coin. If $y=1$ we set $z=x$ otherwise $z=\hat{x}$.

Our task is to build a predictior, $f$, which receives as input $z$ and infers the value of $y$ (outputs the probability that its value is $1$). In other words, $f$ tries to guess the correct ordering of the chunks that make up the randomly scrambled datapoint $z$, thereby solving the jigsaw puzzle. The accuracy of the predictor is evaluated using the log-loss, a.k.a. binary cross-entropy, as it is common in binary classification problems:

$$ \mathcal{L}(f) = - \frac{1}{2} \mathbb{E}_{x\sim P} \left[\log f(x) + \log (1 - f(\hat{x}))\right] $$

Let's consider the case when we express the predictor $f$ in terms of a generative model $Q$ of $x$. $Q$ is an approximation to $P$, and has some parameters $\theta$ which we can tweak. For a given $\theta$, the posterior predictive distribution of $y$ takes the following form:

$$ f(z,\theta) := Q(y=1\vert z;\theta) = \frac{Q(z;\theta)}{Q(z;\theta) + Q(\hat{z};\theta)}, 
$$

where $\hat{z}$ denotes the scrambled/permuted version of $z$. Notice that when $f$ is defined this way the following property holds:

$$ 1 - f(\hat{x};\theta) = f(x;\theta), 
$$

so we can simplify the expression for the log-loss to finally obtain:

\begin{align} \mathcal{L}(\theta) &= - \mathbb{E}_{x \sim P} \log Q(x;\theta) + \mathbb{E}_{x \sim P} \log [Q(x;\theta) + Q(\hat{x};\theta)]\\ &= \operatorname{KL}[P\|Q_{\theta}] - \operatorname{KL}\left[P\middle\|\frac{Q_{\theta}(x)+Q_{\theta}(\hat{x})}{2}\right] + \log(2) \end{align}

So we already see that using the jigsaw objective to train a generative model reduces to minimising the difference between two KL divergences. It's also possible to reformulate the loss as:

$$ \mathcal{L}(\theta) = \operatorname{KL}[P\|Q_{\theta}] - \operatorname{KL}\left[\frac{P(x) + P(\hat{x})}{2}\middle\|\frac{Q_{\theta}(x)+Q_{\theta}(\hat{x})}{2}\right] - \operatorname{KL}\left[P\middle\|\frac{P(x) + P(\hat{x})}{2}\right] + \log(2) $$

Let's look at what the different terms do:

- The first term is the usual KL divergence that would correspond to maximum likelihood. So it just tries to make $Q$ as close to $P$ as possible.
- The second term is a bit weird, particularly as comes into the formula with a negative sign. The KL divergence is $0$ if $Q$ and $P$ define the distribution over the set of jigsaw pieces ${x_1,x_2}$. Notice, I used set notation here, so the ordering does not matter. In a way this term tells the loss function: don't bother modelling what the jigsaw pieces are, only model how they fit together.
- The last terms are constant wrt. $\theta$ so we don't need to worry about them.

#### Not a proper scoring rule (and it's okay)

From the formula above it is clear that the jigsaw training objective wouldn't be a proper scoring rule, as it is not uniquely minimised by $Q=P$ in all cases. Here are two counterexamples where the objective fails to capture all aspects of $P$:

Consider the case when $P=\frac{P(x) + P(\hat{x})}{2}$, that is, when $P$ is completely insensitive to the ordering of jigsaw pieces. As long as $Q$ also has this property $Q = \frac{Q(x) + Q(\hat{x})}{2}$, all KL divergences are $0$ and the jigsaw objective is constant with respect $\theta$. Indeed, it is impossible in this case for any classifier to surpass chance level in the jigsaw problem.

Another simple example to consider is a two-dimensional binary $P$. Here, the jigsaw objective only cares about the value of $Q(0,1)$ relative to $Q(1,0)$, but completely insensitive to $Q(1,1)$ and $Q(0,0)$. In other words, we don't really care how often $0$s and $1$s appear, we just want to know which one is likelier to be on the left or the right side.

This is all fine because we don't use this technique for generative modelling. We want to use it for representation learning, so it's okay to ignore some aspects of $P$.

#### Representation learning

I think this method seems like a really promising direction for unsupervised representation learning. In my mind representation learning needs either:

- strong prior assumptions about what variables/aspects of data are behaviourally relevant, or relevant to the tasks we want to solve with the representations.
- at least a little data in a semi-supervised setting to inform us about what is relevant and what is not.

Denoising autoencoders (with L2 reconstruction loss) and maximum likelihood training try to represent all aspects of the data generating distribution, down to pixel level. We can encode further priors in these models in various ways, either by constraining the network architecture or via probabilistic priors over latent variables.

The jigsaw method encodes prior assumptions into the training procedure: that the structure of the world (relative position of parts) is more important to get right than the low-level appearance of parts. This is probably a fair assumption.

**Dropout for layers** sums it up pretty well. The authors built on the idea of [deep residual networks](http://arxiv.org/abs/1512.03385) to use identity functions to skip layers. 

The main advantages:

* Training speed-ups by about 25%
* Huge networks without overfitting

## Evaluation

* [CIFAR-10](https://www.cs.toronto.edu/~kriz/cifar.html): 4.91% error ([SotA](https://martin-thoma.com/sota/#image-classification): 2.72 %) Training Time: ~15h
* [CIFAR-100](https://www.cs.toronto.edu/~kriz/cifar.html): 24.58% ([SotA](https://martin-thoma.com/sota/#image-classification): 17.18 %) Training time: < 16h
* [SVHN](http://ufldl.stanford.edu/housenumbers/):  1.75% ([SotA](https://martin-thoma.com/sota/#image-classification): 1.59 %) - trained for 50 epochs, begging with a LR of 0.1, divided by 10 after 30 epochs and 35. Training time: < 26h