Wasserstein GAN
Martin Arjovsky and Soumith Chintala and Léon Bottou
arXiv e-Print archive - 2017 via Local arXiv
Keywords: stat.ML, cs.LG
First published: 2017/01/26 (7 years ago)
Abstract: We introduce a new algorithm named WGAN, an alternative to traditional GAN training. In this new model, we show that we can improve the stability of learning, get rid of problems like mode collapse, and provide meaningful learning curves useful for debugging and hyperparameter searches. Furthermore, we show that the corresponding optimization problem is sound, and provide extensive theoretical work highlighting the deep connections to other distances between distributions.
more
less
Martin Arjovsky and Soumith Chintala and Léon Bottou
arXiv e-Print archive - 2017 via Local arXiv
Keywords: stat.ML, cs.LG
First published: 2017/01/26 (7 years ago)
Abstract: We introduce a new algorithm named WGAN, an alternative to traditional GAN training. In this new model, we show that we can improve the stability of learning, get rid of problems like mode collapse, and provide meaningful learning curves useful for debugging and hyperparameter searches. Furthermore, we show that the corresponding optimization problem is sound, and provide extensive theoretical work highlighting the deep connections to other distances between distributions.
|
[link]
This very new paper, is currently receiving quite a bit of attention by the [community](https://www.reddit.com/r/MachineLearning/comments/5qxoaz/r_170107875_wasserstein_gan/). The paper describes a new training approach, which solves the two major practical problems with current GAN training: 1) The training process comes with a meaningful loss. This can be used as a (soft) performance metric and will help debugging, tune parameters and so on. 2) The training process does not suffer from all the instability problems. In particular the paper reduces mode collapse significantly. On top of that, the paper comes with quite a bit mathematical theory, explaining why there approach works and other approachs have failed. This paper is a must read for anyone interested in GANs. 
Your comment:
|
|
[link]
_Objective:_ Robust unsupervised learning of a probability distribution using a new module called the `critic` and the `Earth-mover distance`. _Dataset:_ [LSUN-Bedrooms](http://lsun.cs.princeton.edu/2016/) ## Inner working: Basically train a `critic` until convergence to retrieve the Wasserstein-1 distance, see pseudo-algorithm below: [](https://cloud.githubusercontent.com/assets/17261080/25667162/003c9330-3023-11e7-9081-c181011f4e6f.png) ## Results: * Easier training: no need for batch normalization and no need to fine-tune generator/discriminator balance. * Less sensitivity to network architecture. * Very good proxy that correlates very well with sample quality. * Non-vanishing gradients.  |
|
[link]
* They suggest a slightly altered algorithm for GANs.
* The new algorithm is more stable than previous ones.
### How
* Each GAN contains a Generator that generates (fake-)examples and a Discriminator that discriminates between fake and real examples.
* Both fake and real examples can be interpreted as coming from a probability distribution.
* The basis of each GAN algorithm is to somehow measure the difference between these probability distributions
and change the network parameters of G so that the fake-distribution becomes more and more similar to the real distribution.
* There are multiple distance measures to do that:
* Total Variation (TV)
* KL-Divergence (KL)
* Jensen-Shannon divergence (JS)
* This one is based on the KL-Divergence and is the basis of the original GAN, as well as LAPGAN and DCGAN.
* Earth-Mover distance (EM), aka Wasserstein-1
* Intuitively, one can imagine both probability distributions as hilly surfaces. EM then reflects, how much mass has to be moved to convert the fake distribution to the real one.
* Ideally, a distance measure has everywhere nice values and gradients
(e.g. no +/- infinity values; no binary 0 or 1 gradients; gradients that get continously smaller when the generator produces good outputs).
* In that regard, EM beats JS and JS beats TV and KL (roughly speaking). So they use EM.
* EM
* EM is defined as
* 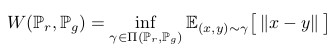
* (inf = infinum, more or less a minimum)
* which is intractable, but following the Kantorovich-Rubinstein duality it can also be calculated via
* 
* (sup = supremum, more or less a maximum)
* However, the second formula is here only valid if the network is a K-Lipschitz function (under every set of parameters).
* This can be guaranteed by simply clipping the discriminator's weights to the range `[-0.01, 0.01]`.
* Then in practice the following version of the tractable EM is used, where `w` are the parameters of the discriminator:
* 
* The full algorithm is mostly the same as for DCGAN:
* 
* Line 2 leads to training the discriminator multiple times per batch (i.e. more often than the generator).
* This is similar to the `max w in W` in the third formula (above).
* This was already part of the original GAN algorithm, but is here more actively used.
* Because of the EM distance, even a "perfect" discriminator still gives good gradient (in contrast to e.g. JS, where the discriminator should not be too far ahead). So the discriminator can be safely trained more often than the generator.
* Line 5 and 10 are derived from EM. Note that there is no more Sigmoid at the end of the discriminator!
* Line 7 is derived from the K-Lipschitz requirement (clipping of weights).
* High learning rates or using momentum-based optimizers (e.g. Adam) made the training unstable, which is why they use a small learning rate with RMSprop.
### Results
* Improved stability. The method converges to decent images with models which failed completely when using JS-divergence (like in DCGAN).
* For example, WGAN worked with generators that did not have batch normalization or only consisted of fully connected layers.
* Apparently no more mode collapse. (Mode collapse in GANs = the generator starts to generate often/always the practically same image, independent of the noise input.)
* There is a relationship between loss and image quality. Lower loss (at the generator) indicates higher image quality. Such a relationship did not exist for JS divergence.
* Example images:
* 
 |
You must log in before you can submit this summary! Your draft will not be saved!
Preview:












